はじめに
最適輸送の理論とアルゴリズムを買って読みました。 Computational Optimal Transportも7割ぐらい読んでたのですが、やっぱり日本語でこういう本があるといいですね。 本の内容のなかでtree-sliced Wassersteinが気になったので、理解のために実装してみます。 以下では、2つの2次元点群間のtree-sliced Wasserstein距離を考えます。 (証明などを含む細かい内容についてはここでは触れません。また、実装は理解のためのものであり遅いです)
Tree-sliced Wasserstein距離
Wasserstein距離は確率分布などの距離を測れるいい感じの距離ですが、計算が重いという問題があります。 Wasserstein距離を高速に計算するためにいくつかの手法が提案されています。 そのうちの1つがtree-sliced Wasserstein距離です。 Tree-sliced Wasserstein距離は木上の最適輸送距離が木のノード数に対して線形時間で解けることを利用することで高速に計算することができます。 点群データに対するtree-sliced Wasserstein距離を計算するためには、はじめに2つの点群データを1つの木で表現する必要があります。 この変換の方法によって、点群上で直接Wasserstein距離を求める場合とtree-sliced Wasserstein距離は異なる値になります。
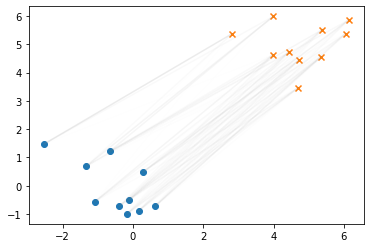
はじめに、以下のような4点ずつの点群(X, Y)間のtree-sliced Wasserstein距離を考えます。
import ot import numpy as np import pylab as plt from sklearn.cluster import AgglomerativeClustering import anytree from anytree import Node, RenderTree from anytree.exporter import DotExporter from IPython.display import Image
X = np.random.randn(4, 2) Y = np.random.randn(4, 2) plt.scatter(X[:,0], X[:,1], label="X", marker="o") plt.scatter(Y[:,0], Y[:,1], label="Y", marker="o") plt.legend()

Tree-sliced Wasserstein距離では、はじめにこの2つの点群を1つの木に変換します。 木に変換する方法はいくつか考えられますが、ここでは以下のように階層クラスタリングを行います。 今回用いたクラスタリング手法では、データ点はすべて葉ノードに含まれます。
XY = np.r_[X,Y] model = AgglomerativeClustering(distance_threshold=0, n_clusters=None, metric="l1", linkage="average") model.fit(XY)
得られたクラスタリング結果を木で表現すると以下のような感じになります。
nodes = [] for i,x_i in enumerate(X): nodes.append(Node("x_%d"%i)) for j,y_j in enumerate(Y): nodes.append(Node("y_%d"%j)) for node_i, children in enumerate(model.children_): nodes.append(Node("%d" % (node_i + len(XY)), children=[nodes[c] for c in children])) root = nodes[-1]
DotExporter(root).to_picture("temp.png") Image("temp.png")

この後のためにprintでも木を表示しておきます。
for pre, fill, node in RenderTree(root): print("%s(%s)" % (pre, node.name))
(14)
├── (11)
│ ├── (x_2)
│ └── (y_2)
└── (13)
├── (8)
│ ├── (x_1)
│ └── (y_0)
└── (12)
├── (x_3)
└── (10)
├── (y_3)
└── (9)
├── (x_0)
└── (y_1)
点群間のWasserstein距離を近似するためには、あるノードから別のノードまでの経路上の距離が対応する2つの点間の距離と近くなる必要があります。 ここでは簡単に、葉ノードの位置はもとの点群の点の位置、それ以外のノードの位置は、そのノードを根とする部分木に含まれる点の位置の平均としました。
nodes = [] for i,x_i in enumerate(X): nodes.append(Node("%d"%i, pos=x_i, nb_nodes=1)) for j,y_j in enumerate(Y): nodes.append(Node("%d"%j, pos=y_j, nb_nodes=1)) for node_i, children in enumerate(model.children_): nb_nodes = sum([nodes[c].nb_nodes for c in children]) nodes.append(Node("%d" % (node_i + len(XY)), children=[nodes[c] for c in children], pos=np.sum([nodes[c].pos * nodes[c].nb_nodes for c in children], axis=0)/nb_nodes, nb_nodes=nb_nodes )) root = nodes[-1]
2次元上にも木をプロットしてみます。緑の点がノードを表しています。
positions = np.array([node.pos for node in nodes]) plt.scatter(positions[:,0], positions[:,1], c="C2", marker=".", label="node") plt.scatter(X[:,0], X[:,1], label="X", marker="o") plt.scatter(Y[:,0], Y[:,1], label="Y", marker="o") for node in nodes: for child in node.children: plt.plot(*zip(node.pos, child.pos), c="gray", lw=0.4) plt.legend()

点群を木で表現することができました。次に、木上のWasserstein距離を計算します。 まず、点群の各点に対応するノード(今回は葉ノード)に質量($\mu, \nu$)を与えます。 ここでは同じ質量を各葉ノードに与えることにします。
nodes = [] for i,x_i in enumerate(X): nodes.append(Node("%d"%i, a_u=1/len(X), b_u=0, pos=x_i, nb_nodes=1)) for j,y_j in enumerate(Y): nodes.append(Node("%d"%j, a_u=0, b_u=1/len(Y), pos=y_j, nb_nodes=1)) for node_i, children in enumerate(model.children_): nb_nodes = sum([nodes[c].nb_nodes for c in children]) nodes.append(Node("%d" % (node_i + len(XY)), children=[nodes[c] for c in children], a_u=0, b_u=0, pos=np.sum([nodes[c].pos * nodes[c].nb_nodes for c in children], axis=0)/nb_nodes, nb_nodes=nb_nodes )) root = nodes[-1]
for pre, fill, node in RenderTree(root): print("%s(%s) mu:%s nu:%s pos:%s" % (pre, node.name, node.a_u, node.b_u, node.pos))
(14) mu:0 nu:0 pos:[0.05533982 0.2128882 ]
├── (11) mu:0 nu:0 pos:[-1.00601231 -0.97207743]
│ ├── (2) mu:0.25 nu:0 pos:[-1.18749779 -0.59495726]
│ └── (2) mu:0 nu:0.25 pos:[-0.82452682 -1.3491976 ]
└── (13) mu:0 nu:0 pos:[0.40912386 0.60787674]
├── (8) mu:0 nu:0 pos:[-0.25630872 0.36544372]
│ ├── (1) mu:0.25 nu:0 pos:[-0.26986513 0.52426891]
│ └── (0) mu:0 nu:0.25 pos:[-0.24275231 0.20661853]
└── (12) mu:0 nu:0 pos:[0.74184015 0.72909325]
├── (3) mu:0.25 nu:0 pos:[ 0.65140353 -0.11594999]
└── (10) mu:0 nu:0 pos:[0.77198569 1.01077434]
├── (3) mu:0 nu:0.25 pos:[1.21127603 1.128238 ]
└── (9) mu:0 nu:0 pos:[0.55234052 0.9520425 ]
├── (0) mu:0.25 nu:0 pos:[0.50610384 0.69303867]
└── (1) mu:0 nu:0.25 pos:[0.5985772 1.21104634]
木$T$とその上の質量(測度)が与えられたとき、木上のWassserstein距離は以下のように求めることができます。 $$ {W}_{d_T} (\mu, \nu) = \sum_{v\in V\setminus {r}} d(v, q(v)) | \mu (\Gamma(v)) - \nu(\Gamma(v)) | $$ ここで、$\Gamma(v)$はノード$v$を根とする部分木を表す。また、$V$はノードの集合、$r$は木の根ノードを表す。 また、$d(v, q(v))$はノード$v$から親ノード$q(v)$までの距離を表しています。
この値はsumをとる順番を工夫することで、$|V|$に対して線形時間で計算することができます。 具体的には根から遠い順に、各ノードの重みを子ノードの重みの合計で更新していきます(本中p206、アルゴリズム5.4)。
depths = [n.depth for n in nodes] s = 0 for node, depth in sorted(zip(nodes, depths), key=lambda x:x[1], reverse=True): node.a_u += sum([n.a_u for n in node.children]) node.b_u += sum([n.b_u for n in node.children]) if node.parent is not None: s += np.sum(np.abs(node.parent.pos - node.pos)) * abs(node.a_u - node.b_u)
print("tree-sliced Wasserstein distance:", s)
tree-sliced Wasserstein distance: 0.9691290075619952
ということで、tree-sliced Wasserstein距離を計算することができました。 各ノードの重みは以下のように更新されています。
for pre, fill, node in RenderTree(root): print("%s(%s) mu:%s nu:%s pos:%s" % (pre, node.name, node.a_u, node.b_u, node.pos))
(14) mu:1.0 nu:1.0 pos:[0.05533982 0.2128882 ]
├── (11) mu:0.25 nu:0.25 pos:[-1.00601231 -0.97207743]
│ ├── (2) mu:0.25 nu:0 pos:[-1.18749779 -0.59495726]
│ └── (2) mu:0 nu:0.25 pos:[-0.82452682 -1.3491976 ]
└── (13) mu:0.75 nu:0.75 pos:[0.40912386 0.60787674]
├── (8) mu:0.25 nu:0.25 pos:[-0.25630872 0.36544372]
│ ├── (1) mu:0.25 nu:0 pos:[-0.26986513 0.52426891]
│ └── (0) mu:0 nu:0.25 pos:[-0.24275231 0.20661853]
└── (12) mu:0.5 nu:0.5 pos:[0.74184015 0.72909325]
├── (3) mu:0.25 nu:0 pos:[ 0.65140353 -0.11594999]
└── (10) mu:0.25 nu:0.5 pos:[0.77198569 1.01077434]
├── (3) mu:0 nu:0.25 pos:[1.21127603 1.128238 ]
└── (9) mu:0.25 nu:0.25 pos:[0.55234052 0.9520425 ]
├── (0) mu:0.25 nu:0 pos:[0.50610384 0.69303867]
└── (1) mu:0 nu:0.25 pos:[0.5985772 1.21104634]
Wasserstein距離、sliced-Wsserstein距離との比較
tree-sliced Wasserstein距離が求められるようになったので、これを点群間の普通のWasserstein距離、および、同じくWasserstein距離を近似する方法の1つであるsliced-Wasserstein距離と比較します。
def calc_tree_Wass(X, Y): XY = np.r_[X,Y] model = AgglomerativeClustering(distance_threshold=0, n_clusters=None, metric="l1", linkage="average") model.fit(XY) nodes = [] for i,x_i in enumerate(X): nodes.append(Node("%d"%i, a_u=1/len(X), b_u=0, pos=x_i, nb_nodes=1)) for j,y_j in enumerate(Y): nodes.append(Node("%d"%j, a_u=0, b_u=1/len(Y), pos=y_j, nb_nodes=1)) for node_i, (children, d) in enumerate(zip(model.children_, model.distances_)): nb_nodes = sum([nodes[c].nb_nodes for c in children]) nodes.append(Node("%d" % (node_i + len(XY)), children=[nodes[c] for c in children], a_u=0, b_u=0, pos=np.sum([nodes[c].pos * nodes[c].nb_nodes for c in children], axis=0)/nb_nodes, nb_nodes=nb_nodes )) root = nodes[-1] depths = [n.depth for n in nodes] s = 0 for node, depth in sorted(zip(nodes, depths), key=lambda x:x[1], reverse=True): node.a_u += sum([n.a_u for n in node.children]) node.b_u += sum([n.b_u for n in node.children]) if node.parent is not None: s += np.sum(np.abs(node.parent.pos - node.pos)) * abs(node.a_u - node.b_u) return s
def calc_all(X, Y): tree_wass = calc_tree_Wass(X,Y) # 1-Wasserstein M = np.sum(abs(X[:, None] - Y[None]), axis=2) wass = ot.emd2(np.ones(len(X))/len(X), np.ones(len(Y))/len(Y), M) # sliced Wasserstein sliced_wass = ot.sliced.sliced_wasserstein_distance(X, Y, np.ones(len(X))/len(X), np.ones(len(Y))/len(Y), p=1) return wass, tree_wass, sliced_wass
適当な点群を2つ作って3つの距離をそれぞれ計算してみます。
distances_bias = [] for bias in np.linspace(0, 5, 10): for _ in range(10): X = np.random.randn(101, 2) Y = np.random.randn(100, 2) + bias distances_bias.append(calc_all(X,Y)) distances_bias = np.array(distances_bias)
plt.scatter(X[:,0], X[:,1], label="X", marker=".") plt.scatter(Y[:,0], Y[:,1], label="Y", marker=".") plt.legend()

plt.scatter(distances_bias[:,0], distances_bias[:,1], marker=".", c="C2", label="tree-sliced") plt.scatter(distances_bias[:,0], distances_bias[:,2], marker=".", c="C3", label="sliced") plt.plot([0,10], [0,10], c="gray") plt.legend() plt.xlabel("1-Wasserstein distance") plt.ylabel("(tree) sliced-Wasserstein distance")

横軸がWasserstein距離、縦軸がその他の2つの距離です。また、グレーの線がWasserstein距離を表しています。 図からわかるように、tree-sliced Wasserstein距離は常にWasserstein距離よりも大きな値になってしまいました。
本には書いてなかったので間違っているかもしれませんが、直感的にはtree-sliced Wasserstein距離とWasserstein距離が一致するためには、2つの葉ノードを結ぶ経路上の距離の合計が、もとの点群の対応する2つの点間の距離と一致する必要があるような気がします。一方で、今回行ったノードに対する座標の与え方では、三角不等式から経路上の距離は常にもとの点間の距離以上の値になってしまいます(いくつか上の世代の親ノードの座標を一旦経由してからもう一方のノードの座標に移動するので)。このため、tree-sliced Wasserstein距離のほうが値が大きくなってしまったのだと思われます。
別の傾向をもった点群に対しても3つの距離を求め、比較してみます。
distances_var = [] for var in np.linspace(0, 5, 10): for _ in range(10): X = np.random.randn(101, 2) Y = np.random.randn(100, 2) * var distances_var.append(calc_all(X,Y)) distances_var = np.array(distances_var)
plt.scatter(X[:,0], X[:,1], label="X", marker=".") plt.scatter(Y[:,0], Y[:,1], label="Y", marker=".") plt.legend()

plt.scatter(distances_bias[:,0], distances_bias[:,1], marker=".", c="C2", label="tree-sliced (bias)") plt.scatter(distances_var[:,0], distances_var[:,1], marker=".", c="C4", label="tree-sliced (var)") plt.scatter(distances_bias[:,0], distances_bias[:,2], marker=".", c="C3", label="sliced (bias)") plt.scatter(distances_var[:,0], distances_var[:,2], marker=".", c="C5", label="sliced (var)") plt.plot([0,10], [0,10], c="gray") plt.xlabel("1-Wasserstein distance") plt.ylabel("tree-sliced Wasserstein distance") plt.legend()

sliced Wasserstein距離はデータの性質によらず、同じような傾向がありましたが、tree-sliced Wasserstein距離はデータの性質によって距離が変わってしまいました。階層クラスタリングのやり方が良くないことが原因かなと思いますが、今回はここまでです。 本によると、quadtreeを使ってクラスタリングすると近似度に理論保証があるらしいです。
まとめ
最適輸送の理論とアルゴリズムを読む中で気になったtree-sliced Wasserstein距離を理解のために実装してみました。 実装ミスってる可能性もありますが、何やってるかわかった気がします。 木の作り方に距離の性質がかなり依存しているので、別のクラスタリング手法なども試してみたいです