概要

関係データ学習の学習のために，自分で実装して理解する．ツイッターのフォローフォロワー関係を使って，グラフラプラシアンを求めスペクトルクラスタリングを行った．その結果，なんとなくクラスタリングできた．また，確率的ブロックモデルによる非対称データクラスタリングをStanによって実装しようとした．これはうまくいっていない．

はじめに

関係データ学習という本を買って読んでいる．

www.kspub.co.jp

本の内容は前半と後半に分かれていて，前半は関係データをスペクトルクラスタリングしたり，確率的ブロックモデルでクラスタリングしたりする話．後半は行列分解やテンソル分解の話になっている．まだ前半の途中までしか読めていないが，予想していたよりも数式が簡単だったこともあり，実際のデータに適用してみたくなった．数年前に書いたツイッターのフォローフォロワー関係をダウンロードするスクリプトを見つけたので，これを使ってデータを作り，自分のフォロー中の人たちをクラスタリングしてみることにした． (カット最小化とスペクトルクラスタリングの関係とか，まだよく理解できてないので，理論的な説明はしない．)

ツイッターデータのダウンロード

tweepyを使って関係データをダウンロードする．スクリプトは何年も前に書いたものであり，なんとなく恥ずかしいのでここでは省略するが，

自分がフォローしている人のフォローしている人を全てダウンロード．
ダウンロードした中から自分がフォローしている人たちの関係を抜き出す．

ようになっている．ツイッターのapi制限があるので，100人ちょっとだけど，それなりに時間がかかる．

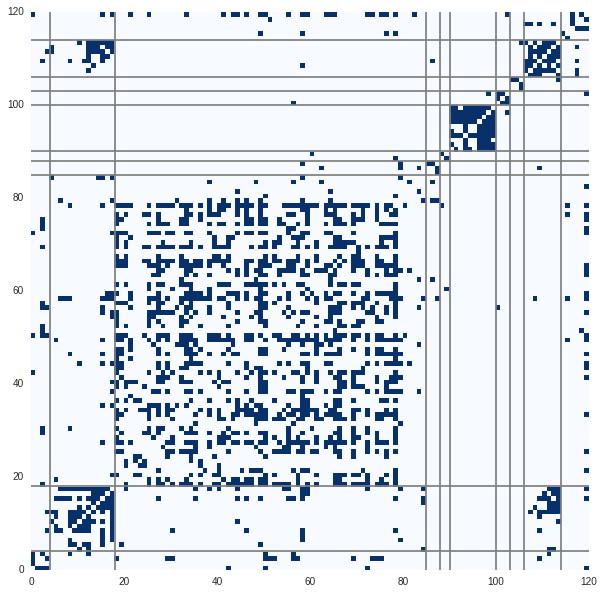
ダウンロードしたのは以下のようなデータ。つながっている部分が青、ない部分が白。鍵垢のデータはとれてない部分もある。ツイッターではフォローしているがされていないなどの関係もあるので，非対称データになる．

import pandas as pd

data = pd.read_csv("./combinationTable.csv")
uname = data[:1].get_values()[0]

%matplotlib inline
import pylab as plt
import seaborn
import numpy as np

X = (data.get_values()[1:]=="True")

def plot_matrix(matrix, clusters=None):
    f, ax = plt.subplots(figsize=(10, 10))
    plt.pcolor(matrix, cmap=plt.cm.Blues )

    if not clusters is None:
        clusters_diff = np.r_[[0], np.diff(clusters)]
        print clusters_diff
        for i,c in enumerate(clusters_diff):
            if c==1:
                ax.axhline(i, c="grey") #, linewidth=1)
                ax.axvline(i, c="grey")#, linewidth=1)
    plt.savefig("../../temp.svg")
    plt.show()

plot_matrix(X)

f:id:ksknw:20161225112150p:plain

すでにある程度のクラスタができているように見える．これは自分が今まで所属した(ツイッター的意味での)クラスタを表している．自分がフォローした順にアカウントが並んでいるので，右上からだいたいポケモン，大学，大学研究室，研究者みたいな感じ．研究者クラスタ以外は知り合いをフォローしていることが多いので，数が少ない．

はじめはこの関係データを対称データに変換し，2章を参考にしつつスペクトルクラスタリングを行う．以下のように対称データに変換した．

symmetry_X = (X.T + X)
plot_matrix(symmetry_X)

f:id:ksknw:20161225112224p:plain

非正規化グラフラプラシアンに基づくスペクトルクラスタリング

対称データ $X$ とクラスタ数 $K$ が与えられたとき、非正規化グラフラプラシアン $L$ は以下のように定義される。

$L=D-X$

ここで $D$ は次数行列で、オブジェクトから伸びるリンクの総数。 $L$ をプロットすると以下。

D = np.eye(symmetry_X.shape[0]) * symmetry_X.sum(axis=0)
K = 10
L = D - X
plot_matrix(L)

f:id:ksknw:20161225125154p:plain

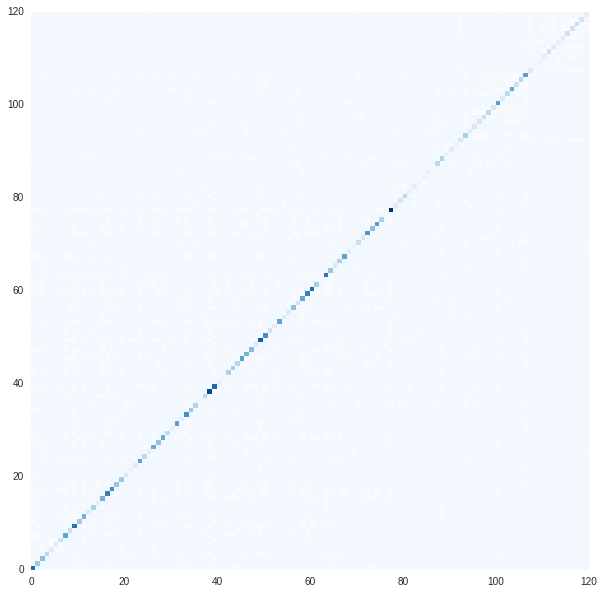
先ほどまでとはグラフの色が異なるので注意．対角成分だけ1以上の値をとるのでこんな感じの図になる。

スペクトルクラスタリングでは、以下の手順でクラスタを抽出する。

グラフラプラシアンを固有値分解して固有ベクトルを求める。
固有ベクトルをK-meansなどでクラスタリングする。

クラスタ数は適当に10とした。本来なら色々チューニングしないといけないが、面倒なので固定する。

import scipy.linalg

hi = K-1
lo = 0
eigen_value,eigen_vector = scipy.linalg.eigh(L,eigvals=(lo,hi))

def plot_eigen_vec(eigen_vector):
    plt.figure(figsize=(30,10))
    plt.plot(np.abs(eigen_vector))
    plt.show()

from sklearn.cluster import KMeans
def kmeans(eigen_vector, unames, n_clusters):
    kmean = KMeans(n_clusters=n_clusters)
    clusters = kmean.fit_predict(eigen_vector)
    cluster_uname = zip(clusters, uname)
    cluster_uname.sort(key=lambda x:x[0])
    print cluster_uname
    return clusters

def sort_by_cluster(matrix, clusters):
    sorted_mat = zip(clusters, matrix)
    sorted_mat.sort(key=lambda x:x[0])
    _,sorted_mat = zip(*sorted_mat)
    
    sorted_mat = zip(clusters, np.array(sorted_mat).T)
    sorted_mat.sort(key=lambda x:x[0])
    sorted_clusters,sorted_mat = zip(*sorted_mat)
    return np.array(sorted_mat).T, sorted_clusters

plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))
sorted_mat, sorted_clusters = sort_by_cluster(symmetry_X, clusters)

クラスタリング結果は以下。クラスタの番号順に並び替えて、境界に線を引いた。

f:id:ksknw:20161225125552p:plain

でかいクラスタが1つと1アカウントしかないクラスタがいくつかできた。正規化しない単純なグラフラプラシアンだとこういう結果になるらしい。

対称正規化グラフラプラシアンに基づくスペクトルクラスタリング

もう少し望ましいクラスタリングを得るために、グラフラプラシアンの正規化を行う。これは(緩和した)グラフカットの正規化と等価になる(?)らしいが、細かい説明は本(とその参考文献)に譲る。読まねば。

対象正規化グラフラプラシアン $L_\mathrm{sym}$ は、上で定義したグラフラプラシアン $L$ から以下のように求まる。

$L_\mathrm{sym} =D^{-\frac{1}{2}} L D^{-\frac{1}{2}}$

L = D - X
L_sym = np.dot(np.dot(scipy.linalg.sqrtm(np.linalg.inv(D)) , L) , scipy.linalg.sqrtm(np.linalg.inv(D))) # D**(-0.5) * L * D**(-0.5)
plot_matrix(L_sym)
eigen_value,eigen_vector = scipy.linalg.eigh(L_sym,eigvals=(lo,hi))
eigen_vector = eigen_vector/np.linalg.norm(eigen_vector)

対象正規化グラフラプラシアンのプロットは以下。非正規化グラフラプラシアンに比べて対角項が小さくなっている。また、クラスタリングする前に固有ベクトルを正規化している。

f:id:ksknw:20161225144212p:plain

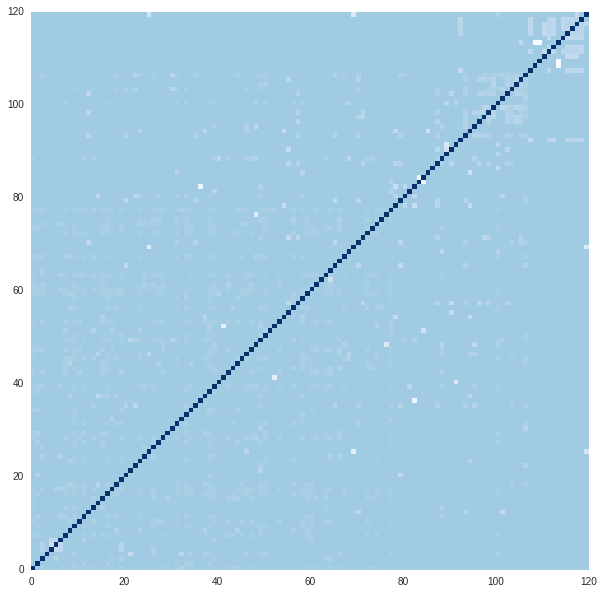
plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))

クラスタリング結果は以下。先程に比べればだいぶ良さそうだが、真ん中の巨大なクラスタにほとんど周りとつながっていないものがいくつか含まれている。

f:id:ksknw:20161225144619p:plain

酔歩正規化グラフラプラシアン

別の正規化から導かれるグラフラプラシアンを使ってクラスタリングをする。

$L_\mathrm{rw} =D^{-1} L$

L = D - X
L_rw = np.dot(np.linalg.inv(D) , L)  # D**(-1) * L 

plot_matrix(L_rw)
eigen_value,eigen_vector = scipy.linalg.eigh(L_rw,eigvals=(lo,hi))

plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))

f:id:ksknw:20161225145741p:plain

でかいクラスタが少し分割されて、まあこっちのほうがいいかなぁという感じ。

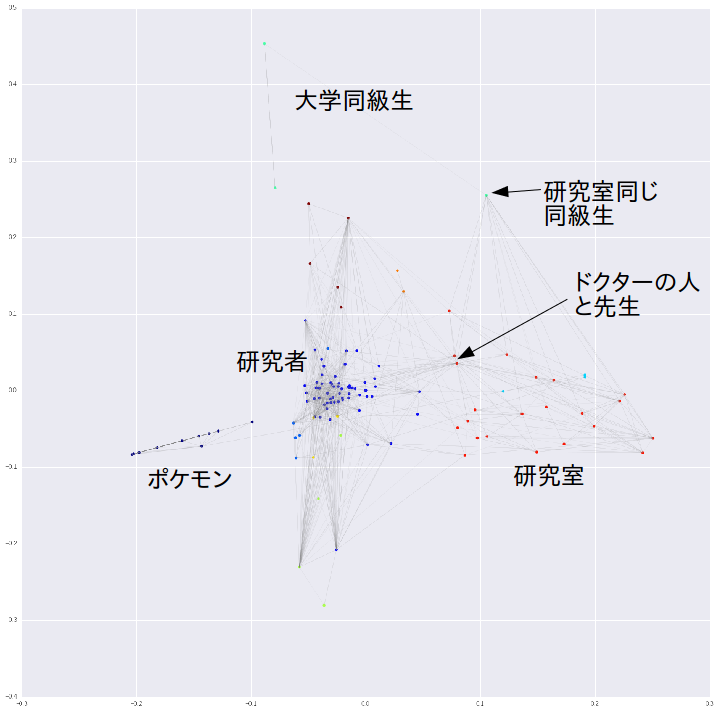
固有ベクトルをPCAで2次元に落としてプロットする。左でポケモンクラスタが孤立している。右に研究室のクラスタがきた。ドクターの人と先生のアカウントは研究者のクラスタとエッジをたくさんもっている。研究室が同じかつ大学の同級生は大学同級生クラスタと研究室クラスタの間に配置された。このような感じで、まあまあ妥当なクラスタリングができた。

from sklearn.decomposition import PCA
# from sklearn.manifold import TSNE
# decomp = TSNE()
decomp = PCA()
decomped = decomp.fit_transform(eigen_vector)

%matplotlib inline
plt.figure(figsize=(20,20))
for i,row in enumerate(X):
    for j,is_connected in enumerate(row):
        if is_connected:
            plt.plot(decomped[[i,j], 0], decomped[[i,j], 1], alpha=0.2,linewidth=0.3, c="gray")
plt.scatter(decomped[:,0], decomped[:,1], c=clusters, linewidths=0, cmap=plt.cm.jet)
#for d,u in zip(decomped, uname):
#    plt.text(d[0], d[1], u)
plt.show()

f:id:ksknw:20161229121731p:plain

確率的ブロックモデルによる非対称データクラスタリング

ここまでは、本来非対称データであるツイッターの関係データを対称データとしてクラスタリングした。ここからは、確率的ブロックモデル(SBM)を使って非対称データのままクラスタリングする。

$i$ 番目のアカウントが $j$ 番目のアカウントをフォローしているかどうかを ${ \displaystyle x_{i,j} }$ と書く。また、 $z_{1,i}$ を $i$ 番目のアカウントが所属するフォローする側のクラスタ、 $z_{2,i}$ をフォローされる側のクラスタとする。フォローする側のクラスタとか意味がわからないかもしれないが、例えば機械学習関連のアカウントをフォローしまくっているクラスタとかそういう感じだと思う。

このときSBMでは以下の生成モデルを仮定する。

$\pi_1 \mid \alpha_1 \sim \mathrm{Dirichlet}(\alpha_1)$
$\pi_2 \mid \alpha_2 \sim \mathrm{Dirichlet}(\alpha_2)$
$z_{1,i} = k\mid \pi_1 \sim \mathrm{Discrete}(\pi_1)$
$z_{2,i} = l\mid \pi_2 \sim \mathrm{Discrete}(\pi_2)$
$\theta_{k,l} \mid a_0,b_0 \sim \mathrm{Beta}(a_0,b_0)$
${ \displaystyle x_{i,j} \mid {\theta_{k,l}} , z_{1,i}, z_{2,j} \sim \mathrm{Bernoulli}(\theta_{z_{1,i}, z_{2,j}}) }$

SBMを使うと、「フォローする(1)」と「フォローされる(2)」にわけてクラスタを考えることになる。例えば「フォロワーするクラスタ」は有名な研究者をフォローするクラスタだが、「フォローされるクラスタ」は研究室の人とかそういうことになる。うっ

SBMでは、クラスタ間の関係の強さ $\theta_{k,l}$ とそれぞれのアカウントがどのクラスタに所属するか $z_{1,i}$ 、 $z_{2,i}$ を同時に推定する。本では周辺化ギブスサンプラーによる推論方法の導出を行っている。ここでは、Stanを用いて、SBMを解くことを試みる。まずは、上の数式をそのままStanに変換すると以下のようになる。

data{
  int N;
  int K;
  int x[N, N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  int z1[N];
  int z2[N];
  vector[K] pi1;
  vector[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  matrix[K,K] theta;
}

model{
  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);

  for (i in 1:N){
    z1[i] ~ categorical(pi1);
    z2[i] ~ categorical(pi2);
  }

  for (k in 1:K){
    for(l in 1:K){
      theta[k,l] ~ beta(a0, b0);
    }
  }

  for (i in 1:N){
    for (j in 1:N){
      x[i,j] ~ bernoulli(theta[z1[i], z2[j]]);
    }
  }
}

これには色々問題があるが、特にint型の変数がparametersの中に含まれていることが問題である。 Stanでは離散的なパラメータを扱うことができないので、zで周辺化する必要がある。 zで周辺化したり、遅すぎないようにベクトルにしたりで以下のようになる。~~(たぶんあっていると思う。)~~間違っている。

data{
  int N;
  int K;
  int x[N*N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  simplex[K] pi1;
  simplex[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  vector<lower=0,upper=1>[K*K] theta;
}

model{
  real gamma[K*K];

  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);
  theta ~ beta(a0, b0);

  for (k in 1:K){
    for (l in 1:K){
      gamma[k+ K*(l-1)] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x | theta[k+ K*(l-1)]);
    }
  }
  target += log_sum_exp(gamma);
}

サンプリングする。

import pystan
data_dict= {"N":len(X),
            "K":10,
            "x":X.astype(int).reshape(-1)}
fit = pystan.stan("sbm_vector.stan", data=data_dict)
fit

            mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
alpha1[0]  2.6e7   3.1e7  5.3e7 3429.6 4934.1  3.9e4  1.2e7  1.8e8    3.0    3.2
alpha1[1]  3.2e8   3.5e8  5.0e8  3.0e5  1.4e6  3.7e7  5.4e8  1.4e9    2.0   6.44
alpha1[2]  1.0e7   6.9e6  9.7e6 460.13  1.1e6  6.9e6  1.5e7  3.4e7    2.0    2.7
alpha1[3]  2.9e7   3.6e7  5.0e7 9752.8  2.5e4  7.6e5  4.8e7  1.4e8    2.0   9.99
alpha1[4]  9.3e6   1.2e7  1.6e7   1.29  5.7e4  3.8e5  9.9e6  5.1e7    2.0   5.75
...
theta[97]   0.58    0.14   0.25   0.16    0.3    0.6   0.74   0.98    3.0   3.63
theta[98]   0.29    0.04   0.16   0.02   0.23   0.23   0.35   0.78   17.0   1.12
theta[99]   0.35    0.09   0.16   0.11   0.19   0.34   0.54   0.57    3.0   2.23
lp__       -4015   40.35  57.06  -4105  -4053  -4019  -3975  -3929    2.0  12.14

fit.plot()

f:id:ksknw:20161229165851p:plain

うまく収束しなかった。特に対策をしていないために、ラベルスイッチングが起こっているのが原因かなと思ったので、 $\theta$ の片側をorderに変えた。 0~1の制約も残さないといけないので、すこしごちゃごちゃした。

data{
  int N;
  int K;
  int x[N*N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  simplex[K] pi1;
  simplex[K] pi2;
  real mu;
  real<lower=0> sigma;
  ordered[K] theta_l[K];
}

transformed parameters{
  vector<lower=0, upper=1>[K] theta[K];
  for (k in 1:K){
    for (l in 1:K){
      theta[k][l] = inv_logit(theta_l[k][l]);
    }
  }
}

model{
  real gamma[K*K];
  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);
  for (k in 1:K)
    theta_l[k] ~ normal(mu, sigma);

  for (k in 1:K){
    for (l in 1:K){
      gamma[k+ K*(l-1)] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x | theta[k][l]);
    }
  }
  target += log_sum_exp(gamma);
}

サンプリングする。

fit2 = pystan.stan("sbm2.stan", data=data_dict)
fit2

                   mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
    alpha1[0]     2.3e7   1.3e7  2.3e7 6866.1  1.7e6  1.7e7  3.5e7  7.8e7    3.0   2.35
    alpha1[1]     4.4e7   2.0e7  3.4e7  2.1e4  7.3e6  4.3e7  6.1e7  1.1e8    3.0    2.5
    alpha1[2]     3.8e8   5.0e8  7.0e8  2.4e5  1.4e6  4.0e6  4.0e8  2.2e9    2.0   2.96
    alpha1[3]     3.6e7   3.6e7  5.1e7  5.1e6  7.1e6  9.3e6  3.9e7  1.7e8    2.0   3.64
    alpha1[4]     6.1e7   6.1e7  1.1e8  5.6e5  1.1e6  8.5e6  5.7e7  3.5e8    3.0   4.63
    alpha1[5]     3.9e7   3.6e7  5.1e7 2659.3 9569.2  8.9e6  6.2e7  1.5e8    2.0   4.23
    ...
    theta[8,9]     0.95    0.07   0.13   0.51    1.0    1.0    1.0    1.0    4.0   1.66
    theta[9,9]     0.93    0.08   0.16   0.38    1.0    1.0    1.0    1.0    4.0    1.8
    lp__          -4060    6.59  13.17  -4087  -4070  -4060  -4049  -4039    4.0   1.98

が、これもだめ。

諦めて一端ここで終わり。

追記(2017年1月5日)

上記はたぶん間違っているので、以下のようなモデルを作った。しかし、これもうまくいっていない。

data{
  int N;
  int K;
  int x[N,N];
}

parameters{
  simplex[K] pi1;
  simplex[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  /* vector<lower=0>[K] alpha1; */
  /* vector<lower=0>[K] alpha2; */
  matrix<lower=0, upper=1>[K,K] theta;
}

transformed parameters{
  matrix<upper=0>[K,K] soft_z[N, N];
  for (i in 1:N){
    for (j in 1:N){
      for (k in 1:K){
        for (l in 1:K){
          soft_z[i,j, k,l] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x[i,j] | theta[k,l]);
        }
      }
    }
  }
}

model{
  /* pi1 ~ dirichlet(alpha1); */
  /* pi2 ~ dirichlet(alpha2); */
  to_vector(theta) ~ beta(a0, b0);

  for (i in 1:N){
    for (j in 1:N){
      target += log_sum_exp(soft_z[i,j]);
    }
  }
}