DTW (動的時間伸縮法)の実装
概要
自分の勉強のために、Dynamic Time Warpingを実装した。 正弦波データでいろいろプロットした後、気温のデータに適用した。 たぶんバグってないと思う。
はじめに
時系列データの類似度(距離)を計算するとき、単純には例えば各時刻での二乗誤差の平均などを求めることを思いつくが、これは以下のようなデータに対して、直感に反する結果になる。
%matplotlib inline import numpy as np import pylab as plt import seaborn as sns
T = 150 t = .4 A = np.sin(np.array(range(T))/10) B = np.sin((np.array(range(T))/10 + t*np.pi)) C = np.zeros((T)) plt.plot(A) plt.plot(B) plt.plot(C) plt.show()
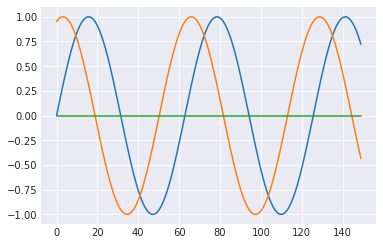
これら3つの時系列データ間の平均二乗誤差を求めると以下のようになる。
mse = lambda a,b: ((a-b)**2).mean() print("A-B: ", mse(A,B)) print("A-C: ", mse(A,C))
A-B: 0.663947047674
A-C: 0.515002685544
この結果から、青とオレンジよりも青と緑のほうが近いということになる。 これは直感に反するので、もう少し上手く距離(的なもの)を定義したい。
Dynamic Time Warping
Dynamic Time Warping (DTW)は2つの時系列データ間の距離(的なもの)を求めるアルゴリズム。
具体的には2つ時系列データの時刻をt1, t2とすると、t1,t2全ての組の誤差を計算し、それらの合計が最小になるような経路を求めるアルゴリズムになっている。
こちらのブログにアニメーションがあって良かった。
以下では、これを参考にして実装する。 書いてあったアルゴリズムをできるだけそのまま書こうと思ったのでギリシャ文字とかを使っている。
δ = lambda a,b: (a - b)**2 first = lambda x: x[0] second = lambda x: x[1] def minVal(v1, v2, v3): if first(v1) <= min(first(v2), first(v3)): return v1, 0 elif first(v2) <= first(v3): return v2, 1 else: return v3, 2 def calc_dtw(A, B): S = len(A) T = len(B) m = [[0 for j in range(T)] for i in range(S)] m[0][0] = (δ(A[0],B[0]), (-1,-1)) for i in range(1,S): m[i][0] = (m[i-1][0][0] + δ(A[i], B[0]), (i-1,0)) for j in range(1,T): m[0][j] = (m[0][j-1][0] + δ(A[0], B[j]), (0,j-1)) for i in range(1,S): for j in range(1,T): minimum, index = minVal(m[i-1][j], m[i][j-1], m[i-1][j-1]) indexes = [(i-1,j), (i,j-1), (i-1,j-1)] m[i][j] = (first(minimum)+δ(A[i], B[j]), indexes[index]) return m
print("A-B: ", calc_dtw(A, B)[-1][-1][0]) print("A-C: ", calc_dtw(A, C)[-1][-1][0])
A-B: 9.67371629972
A-C: 77.2504028315
無事にA-Bのほうがだいぶ近そうという結果が得られた。
なにをやっているのかをプロットを書いて確かめる。
def backward(m): path = [] path.append([len(m)-1, len(m[0])-1]) while True: path.append(m[path[-1][0]][path[-1][1]][1]) if path[-1]==(0,0): break path = np.array(path) return path import matplotlib.gridspec as gridspec def plot_path(path, A, B): gs = gridspec.GridSpec(2, 2, width_ratios=[1,5], height_ratios=[5,1] ) ax1 = plt.subplot(gs[0]) ax2 = plt.subplot(gs[1]) ax4 = plt.subplot(gs[3]) list_δ = [[t[0] for t in row] for row in m] list_δ = np.array(list_δ) ax2.pcolor(list_δ, cmap=plt.cm.Blues) ax2.plot(path[:,1], path[:,0], c="C3") ax1.plot(A, range(len(A))) ax1.invert_xaxis() ax4.plot(B, c="C1") plt.show() for line in path: plt.plot(line, [A[line[0]], B[line[1]]], linewidth=0.2, c="gray") plt.plot(A) plt.plot(B) plt.show()
m = calc_dtw(A, B) path = backward(m) plot_path(path, A, B)
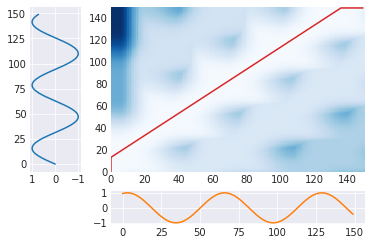
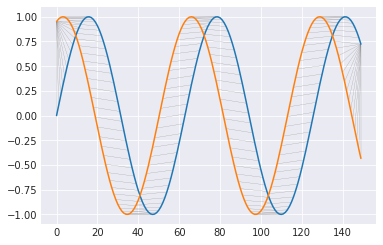
上のグラフは、t1,t2の位置での蓄積した誤差(青)と選択した経路(赤)を表している。横と下のは元の時系列データ。
また、下のグラフは選択した経路によって、2つの時系列データがどのように対応付けられたかを示している。DTWは結局、この対応する2点の(縦方向の)誤差を求めている。最初と最後は対応づけができないので、無理に合わせるしかない。
m = calc_dtw(A, C) path = backward(m) plot_path(path, A, C)
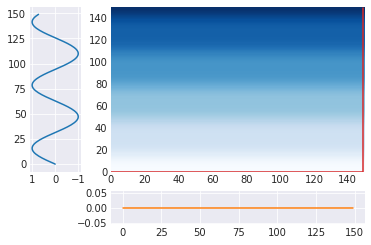
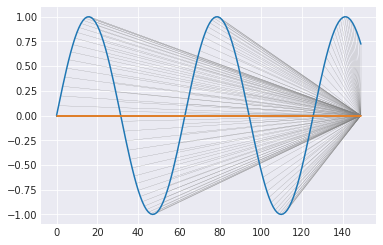
どこに対応づいていても同じだが、実装の関係からこんな感じになっていた。
長さが異なる時系列の距離(的なもの)
DTWは2つの時系列間の対応付けを重複を許す形で行うので、長さの異なる時系列データに対しても問題なく適用できる。
T = 150 S = 200 t = .4 A = np.sin(np.array(range(T))/10) D = np.sin((np.array(range(S))/10 + t*np.pi)) m = calc_dtw(A, D) path = backward(m) plot_path(path, A, D)
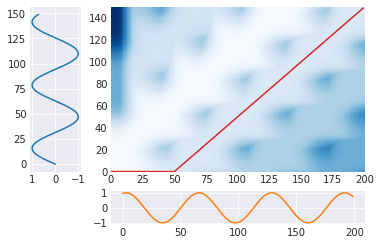
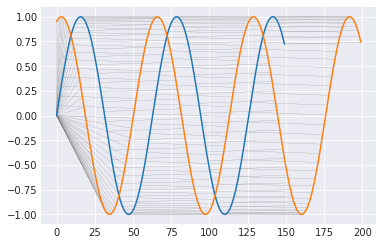
位相をだんだんずらしていったときの挙動
2つの正弦波の位相を徐々にずらしていったときに、MSEおよびDTWが距離(的なもの)をどのように評価するのかをみてみる。
list_dtw_AB = [] list_mse_AB = [] list_dtw_AC = [] list_mse_AC = [] for t in np.arange(0, 2, 0.1): T = 150 A = np.sin(np.array(range(T))/10) B = np.sin((np.array(range(T))/10 + t*np.pi)) list_dtw_AB.append(calc_dtw(A, B)[-1][-1][0]) list_mse_AB.append(mse(A,B)) list_dtw_AC.append(calc_dtw(A, C)[-1][-1][0]) list_mse_AC.append(mse(A,C))
plt.plot(list_mse_AB, label="mse_AB") plt.plot(list_mse_AC, label="mse_AC") plt.legend() plt.show() plt.plot(list_dtw_AB, label="dtw_AB") plt.plot(list_dtw_AC, label="dtw_AC") plt.legend() plt.show()
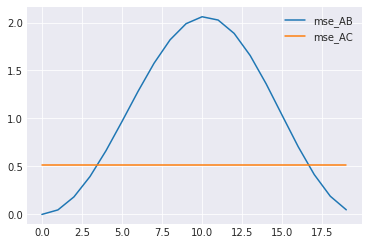
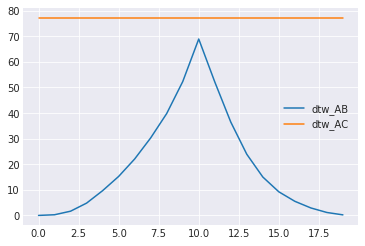
はじめの例で見たようにMSEは位相が少しずれるとy=0のほうが近いと評価してしまう。
DTWも、おそらく端の対応付けから、値は変化するが、y=0のほうが近いと評価されることはない。
(なんで尖ってるんだ...?)
実データ(国内1週間の気温データ)
正弦波ばっかりいじっててもあれなので、気象庁のサイトから適当な地点の1週間分の気温データを落として、各2点間のDTWを求める。
はじめは北海道と沖縄も入れてやったけど、その2つだけ他と離れすぎていて、グラフが見にくかったのでやめた。
また、本当は海外の「同じ時刻」のデータを持ってきて、時差があるけど云々をやりたかったが、めんどくさくなってやめた。
import pandas as pd data = pd.read_csv("./data2.csv", encoding='SHIFT-JIS',skiprows=[0,1, 3,4]) data.index = data["Unnamed: 0"] data = data[data.columns[1::3]] print(data.columns.get_values()) data.head()
['名古屋' '豊中' '八戸' '鹿児島' '福岡' '秋田' '盛岡' '山形' '仙台' '福島' 'つくば(館野)' '宇都宮' 'さいたま'
'千葉' '東京' '新潟' '前橋' '河口湖' '甲府' '静岡' '横浜' '軽井沢' '岐阜' '富山' '金沢' '津' '大津'
'敦賀' '京都' '奈良' '和歌山' '神戸' '岡山' '鳥取' '松江' '呉' '山口' '松山' '高知' '徳島' '高松' '大分'
'宮崎' '熊本' '佐賀' '佐世保']
| 名古屋 | 豊中 | 八戸 | 鹿児島 | 福岡 | 秋田 | 盛岡 | 山形 | 仙台 | 福島 | ... | 山口 | 松山 | 高知 | 徳島 | 高松 | 大分 | 宮崎 | 熊本 | 佐賀 | 佐世保 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unnamed: 0 | |||||||||||||||||||||
| 2017/3/18 1:00:00 | 6.4 | 3.8 | -0.4 | 9.8 | 7.8 | 1.4 | -0.1 | 2.0 | 3.6 | 4.3 | ... | 3.4 | 6.1 | 6.6 | 7.2 | 5.4 | 6.2 | 6.8 | 7.8 | 6.4 | 7.5 |
| 2017/3/18 2:00:00 | 5.3 | 3.4 | -0.4 | 9.5 | 7.0 | 0.9 | 0.0 | 2.2 | 3.3 | 4.7 | ... | 3.0 | 5.6 | 6.0 | 6.4 | 4.7 | 5.9 | 6.8 | 6.1 | 5.9 | 6.8 |
| 2017/3/18 3:00:00 | 5.7 | 2.7 | 0.0 | 9.0 | 7.0 | 0.2 | -0.6 | 2.0 | 3.1 | 5.0 | ... | 2.3 | 5.4 | 5.4 | 6.5 | 4.0 | 4.9 | 6.0 | 5.8 | 4.9 | 6.2 |
| 2017/3/18 4:00:00 | 5.2 | 2.1 | 0.5 | 8.4 | 6.3 | 0.2 | -1.3 | 1.5 | 3.0 | 5.8 | ... | 1.9 | 5.3 | 5.2 | 6.0 | 4.1 | 4.2 | 5.6 | 5.3 | 4.9 | 6.1 |
| 2017/3/18 5:00:00 | 4.5 | 2.0 | 0.8 | 9.1 | 6.1 | -0.2 | -0.6 | 0.3 | 3.8 | 5.7 | ... | 1.7 | 4.9 | 4.8 | 4.5 | 3.0 | 3.8 | 5.1 | 4.5 | 4.2 | 5.7 |
5 rows × 46 columns
import matplotlib.font_manager as fm font = {'family' : 'TakaoGothic'} plt.rc('font', **font) data.plot(figsize=(15,6), legend=False) plt.show()

dtw = [] from itertools import product for i,(key1, key2) in enumerate(product(data.columns, data.columns)): dtw.append(calc_dtw(data[key1].get_values(), data[key2].get_values())[-1][-1][0])
dtw = np.array(dtw).reshape(len(data.columns), -1)
fig = plt.figure(figsize=(10,8)) ax = fig.add_subplot(111) ax.set_aspect("equal") plt.pcolor(dtw, cmap=plt.cm.Blues) plt.xlim(xmax=46) plt.ylim(ymax=46) plt.xticks(np.arange(0.5, len(data.columns)+0.5), list(data.columns), rotation=90) plt.yticks(np.arange(0.5, len(data.columns)+0.5), list(data.columns)) plt.colorbar() plt.show()
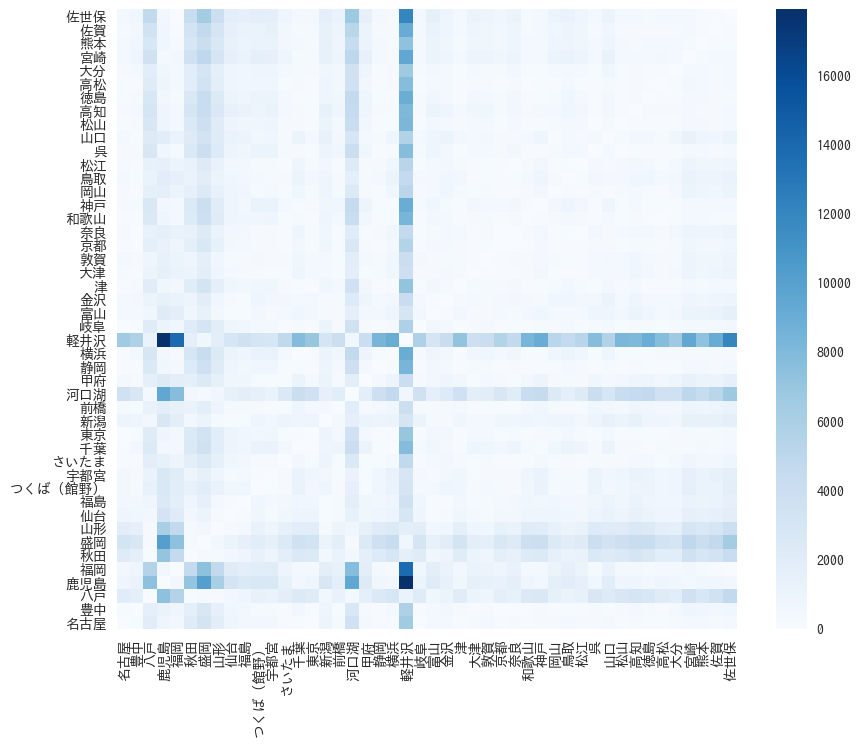
軽井沢、河口湖は他の地点と結構違う。リゾート地ということなんだろうか。
なんとなく東北と九州は気候が結構違うのかなと思った。
おまけ
こういう行列を見ると、ここから色々できそうな気がしてしまう。
tSNE
距離行列あるならtSNEできる気がするので、scikit-learnに突っ込んでみる。
from sklearn.manifold import TSNE tsne = TSNE(metric="precomputed") tsned = tsne.fit_transform(dtw) plt.scatter(tsned[:,0], tsned[:,1]) for d,u in zip(tsned, data.columns): plt.text(d[0], d[1], u)
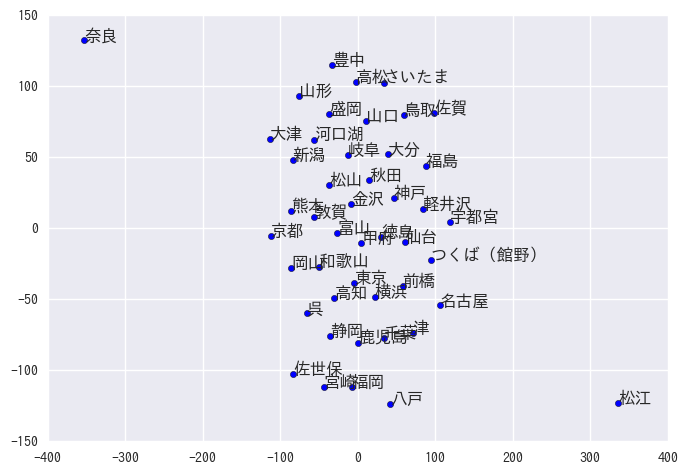
思ってたのと違う図が得られたけど、なんか間違ってる??
スペクトルクラスタリング
類似度という関係データ、しかも対称行列だということでスペクトルクラスタリングをやる。 以前書いたものからコードをコピペしてくる。(みんなノートブックのコードの再利用ってどうしてんの)
import scipy.linalg from sklearn.cluster import KMeans from sklearn.decomposition import PCA def plot_matrix(matrix, clusters=None): f, ax = plt.subplots(figsize=(10, 10)) plt.pcolor(matrix, cmap=plt.cm.Blues ) if not clusters is None: clusters_diff = np.r_[[0], np.diff(clusters)] for i,c in enumerate(clusters_diff): if c==1: ax.axhline(i, c="grey") #, linewidth=1) ax.axvline(i, c="grey")#, linewidth=1) plt.show() def kmeans(eigen_vector, unames, n_clusters): kmean = KMeans(n_clusters=n_clusters) clusters = kmean.fit_predict(eigen_vector) cluster_uname = list(zip(clusters, unames)) cluster_uname.sort(key=lambda x:x[0]) return clusters D = np.eye(dtw.shape[0]) * dtw.sum(axis=0) X = np.mat(dtw) K = 5 hi = K-1 lo = 0 L = D - X L_rw = np.dot(np.linalg.inv(D) , L) # D**(-1) * L eigen_value, eigen_vector = scipy.linalg.eigh(L_rw,eigvals=(lo,hi)) clusters = kmeans(eigen_vector, data.columns, K) decomp = PCA() decomped = decomp.fit_transform(eigen_vector) plt.figure(figsize=(7,7)) plt.scatter(decomped[:,0], decomped[:,1], c=clusters, linewidths=0, cmap=plt.cm.jet) for d,u in zip(decomped, data.columns): plt.text(d[0], d[1], u) plt.show()
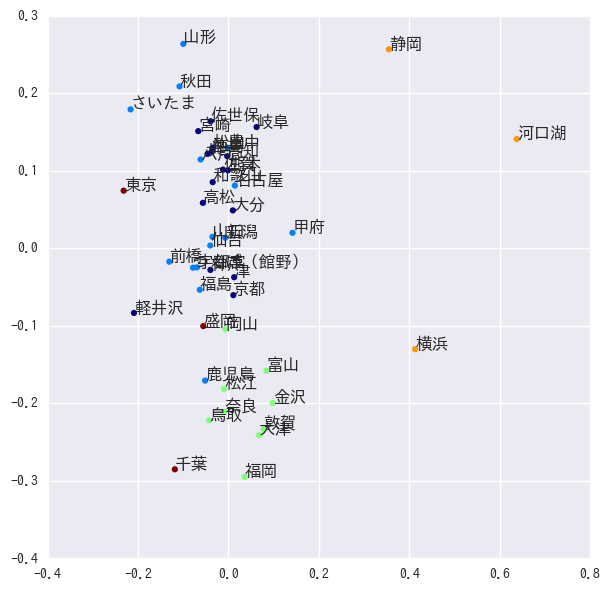
近い地域が同じクラスタになっているかと思ったら、そうでもない部分もあったり。
この1週間は似てたのかもしれないし、本当はデータを見ないとなぁと思いつつ、面倒なので終わり。
おわりに
自分の勉強のためにDTWの実装をやって、色々なデータを突っ込んでみた。 今回はスペクトルクラスタリングをやったけど、参考にした論文やブログでは、重心を求めてkmeansでクラスタリングとかをやっているので、そのあたりもやってみたいなと思う。