Sinkhorn iterationの勾配と輸送行列の関係
はじめに
最近,最適輸送を覚えてちょいちょい使っています. 特にSinkhorn iterationを用いることで,行列計算だけで最適輸送距離をだいたい計算でき,さらに自動微分で勾配が求まるため,色々な問題のロス関数として最適輸送を使うことができます. ところで,最適輸送の式はもともと線形計画問題なので,輸送計画の行列がコストに依存しないとすると,簡単に勾配(らしきもの)を求めることができます. 以下では,自動微分を用いたときと,この方法で求めた勾配を用いたときで,実際にどの程度の差がでるものなのか気になったので,適当なデータに対して両方の手法を適用してみて結果を比較します. 結果,どちらもそんなに変わらないように思えるので,MLのような雑な最適化で済むようなタスクでは自動微分じゃないほうがいいのではないかと思っています. このあたりのことについて,何か知見があれば教えていただけると嬉しいです.
最適輸送問題
適当な2つの2次元空間上の点群$X = \{x_1, \ldots, x_n\}$と$Y = \{y_1, \ldots, y_m\}$の間の最適輸送を考えます.
import numpy as np import pylab as plt from scipy.stats import norm import torch import torch.nn from torch.optim import Adam import ot torch.random.manual_seed(1234)
X = torch.randn(10, 2) Y = torch.randn(10, 2) + np.ones(2)*5 n = X.shape[0] m = Y.shape[0] a = torch.ones(n)/n b = torch.ones(m)/m
plt.scatter(X.detach()[:,0], X.detach()[:,1]) plt.scatter(Y.detach()[:,0], Y.detach()[:,1], marker="x") plt.show()

これらの点群の間の最適輸送問題は以下のように定義されます.ただし,ground metric (点同士の距離)として$L_2$距離の二乗を使います.つまり,$C\in \mathbb R^{n\times m}$の成分$C_{ij} = \|x_i - y_j\|^2_2$です.
$$\min_{P\in U(a,b)} \left \lt P, C \right \gt$$ ここで,$P$は輸送行列で$P_{ij}$は点$x_i$と$y_j$の間の対応関係の強さを表します.$U$は質量保存則を満たす行列の集合であり,$U=\{P\in [0,1]^{n\times m} | P \mathbf 1_m = \mathbf a, P^\top \mathbf 1_n = \mathbf b\}$と書くことができます. $\mathbf a, \mathbf b$はそれぞれ$X, Y$に含まれる各点の重みを表すベクトルです.ここでは単純に各点群に含まれるすべての点が同じ重みを持つとします.つまり$\mathbf a = \mathbf 1_n/n$,$\mathbf b = \mathbf 1_m/{m}$です. 以下ではこの最小化問題の解を輸送コストと呼びます.(輸送コストのrootは2-Wasserstein距離とも呼ばれます.)
この問題は線形計画問題なので,適当なソルバーに突っ込むと,そこそこのサイズの点群に対しても解を求めることができます. しかし,ソルバー(例えば単体法)は微分できないので,輸送コストをロス関数として用いたいなどの機械学習における用途としては使いにくいです. また,点群のサイズを$N$として,計算量も $O({N}^{3})$ かかってしまいます.
そこで,Sinkhorn iterationを使ってエントロピー正則化つきの最適輸送問題を解くということがよくやられています. エントロピー正則化つきの最適輸送問題は以下のように書けます.
$$\min_{P\in U(a,b)} \left \lt P, C \right \gt - H(P)$$
ここで,$H(P)$は輸送行列$P$のエントロピーを表し,$H(P) = - \sum_{i,j} P_{ij} \log P_{ij}$です. $\epsilon$はエントロピー正則化の強さを表します.
この最適化問題に対して,Sinkhorn iterationと呼ばれる反復法を用いて最適解を見つけることができることが知られています. Sinkhorn iterationにはいくつかの表記の仕方がありますが,ここでは後ろの実装と合わせるためにsoftminを用いた表記を用います.
$$ \mathbf f^{(l+1)} = \text{Min}_\epsilon ^{\text{row}} (S(\mathbf f^{(l)}, \mathbf g^{(l)})) + \mathbf f^{(l)} + \epsilon \log(\mathbf a) \\ \mathbf g^{(l+1)} = \text{Min}_\epsilon ^{\text{col}} (S(\mathbf f^{(l+1)}, \mathbf g^{(l)})) + \mathbf g^{(l)} + \epsilon \log(\mathbf b) $$ ここで,$S(\mathbf f, \mathbf g)_{ij} = C_{ij} - f_i - g_j$です. また,$\text{Min}_\epsilon ^{\text{row}}$は行方向へのsoftminを表します.softminは以下の様な関数です.
$$\min_\epsilon \mathbf z = -\epsilon \log \sum_{i} e^{-z_i/\epsilon}$$
$\mathbf f, \mathbf g$を適当に初期化して,この反復を収束するまで行います. その後以下のように$P$を求めることができます.
$$P_{ij} = e^{f_i/\epsilon} e^{-C_{ij}/\epsilon} e^{g_j/\epsilon}$$
では実際に実装して$P$を求めます.
epsilon = 0.01 def softmin(z, epsilon): return -torch.logsumexp(-z/epsilon, dim=1)*epsilon def sinkhorn(C): n,m = C.shape[:2] f = torch.ones(n).double() g = torch.zeros(m).double() C = torch.sum((X[:, None] - Y[None])**2, dim=2) C_max = C.max() C = C/C.max() for i in range(200): S = C - f[:, None] - g[None] f = softmin(S, epsilon=epsilon) + f + epsilon * torch.log(a) S = C - f[:, None] - g[None] g = softmin(S.t(), epsilon=epsilon) + g + epsilon * torch.log(b) P = torch.diag(torch.exp(f/epsilon)) @ torch.exp(-C/epsilon) @ torch.diag(torch.exp(g/epsilon)) return (P * C).sum() * C_max, P
C = torch.sum((X[:, None] - Y[None])**2, dim=2) cost, P = sinkhorn(C)
plt.imshow(P.detach()) plt.show()

plt.scatter(X.detach()[:,0], X.detach()[:,1]) plt.scatter(Y.detach()[:,0], Y.detach()[:,1], marker="x") for i,p_i in enumerate(P): for j,p_ij in enumerate(p_i): plt.plot([X.detach()[i, 0], Y.detach()[j,0]], [X.detach()[i, 1], Y.detach()[j,1]], alpha=float(p_ij.detach().numpy())*2, c="gray") plt.show()
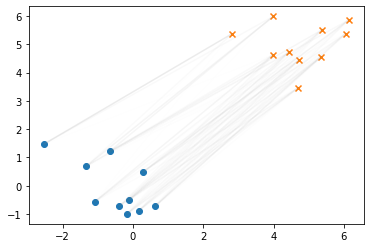
Sinkhorn iterationの微分
先述したように,Sinkhorn iterationは単に行列の掛け算の形で書くことができます (上ではsoftminを使った表記でしたが,softminも$\epsilon>0$で微分可能な関数です). そのため,Sinkhornは微分可能な演算になっています. 実際にpytorchなどを用いると,容易にSinkhornで求まる輸送コストをロスに使ってパラメータの最適化を行うことができます. ここでは簡単に$X$と$Y$の間の輸送コストが小さくなるように$X$を動かしていく問題を,Sinkhorn iterationの勾配を使って解くことを考えます.
original_X = X.clone().detach()
%%time X = original_X.clone().detach() X.requires_grad = True hist_X = [] hist_X.append(X.detach().numpy().copy()) hist_cost = [] optimizer = Adam([X], lr=0.1) for i in range(100): C = torch.sum((X[:, None] - Y[None])**2, dim=2) cost, P = sinkhorn(C) cost.backward() optimizer.step() optimizer.zero_grad() hist_X.append(X.detach().numpy().copy()) hist_cost.append(cost.detach().numpy()) hist_X = np.array(hist_X)
CPU times: user 8.83 s, sys: 8.34 ms, total: 8.84 s
Wall time: 8.86 s
ロスの履歴と移動の軌跡をプロットします.
plt.plot(hist_cost) plt.ylabel("cost") plt.xlabel("iterations") plt.show()

plt.scatter(X.detach()[:,0], X.detach()[:,1]) plt.scatter(Y.detach()[:,0], Y.detach()[:,1], marker="x") plt.scatter(original_X.detach()[:,0], original_X.detach()[:,1], c="C0") plt.plot(hist_X[:,:,0], hist_X[:,:,1], c="C0", lw=0.4, alpha=0.6) plt.show()

左にあった$X$(青点)が$Y$(オレンジ×)の方に移動しているのがわかります. 実際にSinkhorn iterationの微分を使って輸送コストが小さくなるように最適化を実行することができました.
$P$を用いたSinkhornの微分
ようやく本題です. エントロピー正則化つきの場合の輸送コスト$L_\epsilon$は以下のように書くことができます. $$ {L}_{\epsilon} = \big {\lt} {P}^{*}, C \big \gt - \epsilon H(P^{\ast}) $$ ここで,$P^*(C) = \text{argmin}_{P\in U(a,b)} \left \lt P, C \right \gt$ です.
このとき,$L$の$C$に関する微分は以下です. $$ \frac{\partial {L}_{\epsilon}}{\partial C} = P^{\ast}(C) + \frac{\partial P^{\ast} (C)}{\partial C} - \epsilon \frac{\partial H(P^{\ast}(C))}{\partial C} $$ 右辺第2項, 第3項はコストが少し変わったときの最適な輸送行列の変化に依存していますが,例えば勾配を使って点を少しずつ動かすようなタスクでは輸送行列は大体の場合同じで,たまに切り替わるという挙動をしそうな気がします.この場合は,右辺第2,3項は無視しても最適化の結果には大きな影響がないのではないかという気がします.
Sinkhorn iterationsでは自動微分を使って勾配を計算しました.自動微分の計算のためには$f$や$g$の中間値を保存し,かつ,backward計算する必要があります.これに対して$P^*$はSinkhorn iterationsの最後の値を保存しておくだけで計算可能です(そもそもSinkhorn じゃなくても計算できます). 実際にやってみます.
import torch.autograd
class Sinkhorn_P(torch.autograd.Function): @staticmethod def forward(ctx, C): n,m = C.shape[:2] f = torch.ones(n).double() g = torch.zeros(m).double() C_max = C.max() C = C/C.max() for i in range(200): S = C - f[:, None] - g[None] f = softmin(S, epsilon=epsilon) + f + epsilon * torch.log(a) S = C - f[:, None] - g[None] g = softmin(S.t(), epsilon=epsilon) + g + epsilon * torch.log(b) P = torch.diag(torch.exp(f/epsilon)) @ torch.exp(-C/epsilon) @ torch.diag(torch.exp(g/epsilon)) ctx.save_for_backward(P) return (P * C).sum() * C_max, P @staticmethod def backward(ctx, grad_output1, grad_output2): P, = ctx.saved_tensors return P*grad_output1 def sinkhorn_P(C): return Sinkhorn_P.apply(C)
%%time X_P = original_X.clone().detach() X_P.requires_grad = True hist_X_P = [] hist_X_P.append(X_P.detach().numpy().copy()) optimizer = Adam([X_P], lr=0.1) for i in range(100): C = torch.sum((X_P[:, None] - Y[None])**2, dim=2) cost, P = sinkhorn_P(C) cost.backward() optimizer.step() optimizer.zero_grad() hist_X_P.append(X_P.detach().numpy().copy()) hist_X_P = np.array(hist_X_P)
CPU times: user 3.48 s, sys: 3.4 ms, total: 3.48 s
Wall time: 3.48 s
plt.scatter(X_P.detach()[:,0], X_P.detach()[:,1], c="C2") plt.scatter(Y.detach()[:,0], Y.detach()[:,1], marker="x", c="C1") plt.scatter(original_X.detach()[:,0], original_X.detach()[:,1], c="C0") plt.plot(hist_X_P[:,:,0], hist_X_P[:,:,1], c="C2", lw=0.4, alpha=0.6) plt.show()

似たような感じで$X$を更新することができているように見えます.重ねて表示してみます.
plt.scatter(X_P.detach()[:,0], X_P.detach()[:,1], c="C2") plt.scatter(Y.detach()[:,0], Y.detach()[:,1], marker="x", c="C1") plt.scatter(original_X.detach()[:,0], original_X.detach()[:,1], c="C0") plt.plot(hist_X_P[:,:,0], hist_X_P[:,:,1], c="C2", lw=0.4, alpha=0.6) plt.scatter(X_P.detach()[:,0], X_P.detach()[:,1], c="C2") plt.plot(hist_X[:,:,0], hist_X[:,:,1], c="C0", lw=0.4, alpha=0.6) plt.show()

多少軌跡がずれていますが,最終的な収束点はほぼ同じように見えます.また,実行時間はSinkhornの自動微分を用いると10s程度かかっているのに対して,3.8sなので倍以上速くなっています(今回はCPUで実行したのでGPUだとまた違うかも).
おわりに
Sinkrhon iterationをbackwardして求めた勾配と最適な輸送行列を使った勾配っぽいものを比較しました. あんまり真面目に検証してないですが,少なくとも今回のタスクでは$P^*$を勾配として使っても問題なさそうでした. 点群の一致でしか検証してないので,勾配が大きくずれる条件やSinkhorn iterationを真面目にbackpropしない最適化できない問題(凸性が重要なときとか? Pを使うと振動するとか?)があるかもしれません. このあたりのことについて,何か知見があれば教えていただけると嬉しいです.