Entropic neural OT via diffusion process の実装

はじめに

今回は Entropic Neural Optimal Transport via Diffusion Processes (Gushchin+, Neurips2023)について，アルゴリズムを理解することを目的として実装します． 公式の実装はこちらにあります． 最適輸送と拡散モデルの関係については，こちらやこちらがわかりやすかったです．

この論文で提案されているEntropic Neural Optimal Transport (ENOT)では，最適輸送に基づく生成モデルのために，エントロピー正則化つきの最適輸送を拡散モデルっぽいモデル(シュレディンガー橋)を使って解いています． ここでは，最適輸送について説明したあと，拡散モデル，シュレディンガー橋について順に説明し，最後に提案法の説明をします． それぞれの手法について，適当な具体例を用いて実装しつつ理解することを目指します．

準備

最適輸送

最適輸送は2つの分布の間の対応関係を求めたり距離を求めたりするものです． ここでは2つの確率分布$\mathbb P_0$, $\mathbb P_1$の間の最適輸送について考えます．

離散最適輸送

はじめに2つの分布が$\mathbb R^d$次元空間上の離散分布のとき，つまり$\mathbb P_0 = \sum_{i=1}^{N_0}a_i \delta(\boldsymbol x_i), \mathbb P_1 = \sum_{j=1}^{N_1} b_j\delta(\boldsymbol y_j)$のときを考えます．ただし，すべての$i,j$について$\boldsymbol{x}_i, \boldsymbol{y}_j \in \mathbb R^d$です． また，$a_i$，$b_j$は各点の重みを表しています． 実装のための例として，$d=1$とし以下のような2つの分布を$\mathbb P_0, \mathbb P_1$として設定します．

import torch
import numpy as np
import pandas as pd
import pylab as plt
from tqdm import tqdm
import torch
from torch.optim import Adam

import torch.nn as nn
import ot

def P0(t):
    return np.array([np.cos(t*np.pi*2)+0.5, np.sin(t*np.pi*2)+0.5]).T

def P1(t):
    ret = np.zeros((len(t), 2))
    ret[t<0.25,0] = (t*4)[t<0.25]

    ret[np.logical_and(0.25<=t, t<0.5), 0] = 1
    ret[np.logical_and(0.25<=t, t<0.5), 1] = ((t-0.25)*4)[np.logical_and(0.25<=t, t<0.5)]
    
    ret[np.logical_and(0.5 <=t, t<0.75),0] = (1-(t-0.5)*4)[np.logical_and(0.5 <=t, t<0.75)]
    ret[np.logical_and(0.5 <=t, t<0.75),1] = 1
    
    ret[0.75 <=t,0] = 0
    ret[0.75 <=t,1] = (1-(t-0.75)*4)[0.75 <=t]

    return ret

t0 = np.random.rand(40)
t1 = np.random.rand(80)

X0 = P0(t0)
plt.scatter(X0[:,0], X0[:,1])

Y = P1(t1)
plt.scatter(Y[:,0], Y[:,1])

このとき，2つの分布の間の最適輸送は以下のような最適化問題として定義されます． $$ \min_{\pi\in \Pi(\mathbb P_0, \mathbb P_1)}\sum_{i=1}^{N_0} \sum_{j=1}^{N_1}\|\boldsymbol x_i - \boldsymbol y_j\|_2^2 \pi_{ij} $$ ここで，$\pi_{ij}$を$(i,j)$成分にもつ行列$\pi \in [0,1]^{N_0 \times N_1}$は輸送計画と呼ばれるものであり，$\boldsymbol x_i$を$\boldsymbol y_j$と対応づけるか否かを表現しています． $\Pi(\mathbb P_0, \mathbb P_1)$は制約条件を満たす$\pi$の集合を表しています． ここで，制約条件は$\mathbb P_0, \mathbb P_1$の点を過不足なく対応付けることに対応します． 別の言い方として，同時分布$\pi$を周辺化したときに$\mathbb P_0$，$\mathbb P_1$になることを制約しているとも言えます．

この最適化問題は線形計画問題なので，単体法などのソルバーを用いることで解くことができます． 実際に解いてみます．

a = np.ones(len(X0))/len(X0)
b = np.ones(len(Y))/len(Y)
pi = ot.emd(a,b,((X0[:,None]-Y[None])**2).sum(axis=-1))

また，輸送計画(同時分布)$\pi$は以下のような図として書くことができます． 図だとわかりにくいですが、横方向に周辺化すると$\mathbb P_0$，縦方向に周辺化すると$\mathbb P_1$になっています．

plt.imshow(pi)

$\pi_{ij}>0$となっている部分を線で繋いでみると以下のようになります。

X0 = P0(t0)
plt.scatter(X0[:,0], X0[:,1], marker=".")

Y = P1(t1)
plt.scatter(Y[:,0], Y[:,1], marker=".")

for i, xi in enumerate(X0):
    for j,yj in enumerate(Y):        
        if pi[i,j] > 0:
            plt.plot((xi[0], yj[0]), (xi[1], yj[1]), c="gray", lw=0.5)

最適輸送を解くアルゴリズムとしては、このあとで説明するエントロピー正則化を用いることで利用できるSinkhornアルゴリズムという繰り返しアルゴリズムもよく知られています． 離散最適輸送についての詳細はこの本がわかりやすかったです．

連続最適輸送

次に2つの確率分布$\mathbb P_0, \mathbb P_1$が連続分布であり，それぞれの分布からいくつかのサンプルが得られる場合を考えます． 式で書くと以下のようになります． $$ \inf_{\pi \in \Pi(\mathbb P_0, \mathbb P_1)} \int_{\mathcal X\times \mathcal Y} \frac{\|\boldsymbol x - \boldsymbol y\|^2}{2}d\pi(\boldsymbol x, \boldsymbol y) $$ ただし，$\mathcal X, \mathcal Y$はそれぞれ$d$次元のユークリッド空間です． また，$\Pi(\mathbb P_0, \mathbb P_1)$は離散最適輸送の場合と同様に，周辺化すると$\mathbb P_0, \mathbb P_1$になる分布です．

連続分布に対する最適輸送では，輸送計画の行列$\pi$を直接求める代わりに，$\boldsymbol P_0$の点が与えられたときに$\boldsymbol P_1$のどこに輸送されるのかをモデル化した写像を学習することが考えられています． このような学習を行う理由は，連続分布の最適輸送では現在得られているサンプルだけでなく，$\mathbb P_0, \mathbb P_1$から得られる任意のサンプルに対して，どこからどこへ輸送すればよいのかを求めておきたいためです． このような写像をパラメータ$\theta$をもつニューラルネットワーク$T_\theta(\boldsymbol x): \mathcal X\mapsto \mathcal Y$を用いてモデル化することを考えます． $\mathbb P_0$を$T_\theta$によって輸送したときに得られる分布を${T_{\theta}}_\#\mathbb P_0$と書くことにします． このとき，2つの連続分布間の最適輸送は以下のように書くことができます． $$ \inf_{{T_{\theta}}_\#\mathbb P_0=\mathbb P_1} \int_{\mathcal X} \|\boldsymbol x - T_\theta(\boldsymbol x) \|_2^2 d\mathbb P_0(\boldsymbol x) $$ この式は，$\mathbb P_0$をある関数$T_\theta$によって$\mathbb P_1$の形に輸送するとき，なるべく輸送される距離$\|\boldsymbol x - T_\theta(\boldsymbol x)\|_2^2$を小さくするという最適化問題であり，(パラメータ$\theta$をもつ関数でモデル化している点以外は)もともとの最適輸送の問題(1つ上の最適化問題)と同じ問題を考えています．

この最適化問題の解き方にもいくつかの方法がありますが，今回はこのあと実装したいENOTに合わせて，制約条件を緩和した以下の制約なし最適化問題を解くことを考えます． $$ \sup_\phi \inf_{\theta}\int_{\mathcal X} \|\boldsymbol x - T_\theta(\boldsymbol x) \|_2^2 d\mathbb P_0(\boldsymbol x) - \int_{\mathcal Y}\beta_\phi(\boldsymbol y) d{T_{\theta}}_\#\mathbb P_0(\boldsymbol y) + \int_{\mathcal Y} \beta_\phi(\boldsymbol y) d\mathbb P_1(\boldsymbol y) $$ この最適化問題はラグランジュの未定乗数法っぽい変換を用いることで，先程の最適化問題の制約条件を緩和したものです．ただし，$\beta_\phi$はラグランジュ乗数に対応する関数で，これもパラメータ$\phi$を持ったニューラルネットワークを使ってモデル化することにします．

def make_net(n_inputs, n_outputs, n_layers=3, n_hiddens=100):
    layers = [nn.Linear(n_inputs, n_hiddens), nn.ReLU()]

    for i in range(n_layers - 1):
        layers.extend([nn.Linear(n_hiddens, n_hiddens), nn.ReLU()])

    layers.append(nn.Linear(n_hiddens, n_outputs))

    return nn.Sequential(*layers)


lr = 0.0001
n_hidden = 512
nb_epochs = 5000
device = "cpu"

X0 = torch.from_numpy(X0).float().to(device)
Y =  torch.from_numpy(Y).float().to(device) 

f = make_net(n_inputs=2, n_outputs=2, n_layers=3, n_hiddens=n_hidden).to(
    device
)
beta = make_net(n_inputs=2, n_outputs=1, n_layers=3, n_hiddens=n_hidden).to(
    device
)
optim_beta = Adam(beta.parameters(), lr=lr)
optim_f = Adam(f.parameters(), lr=lr)

for i in tqdm(range(nb_epochs)):
    Xn = f(X0)
    Lb = beta(Xn).mean() - beta(Y).mean()
    Lb.backward()
    optim_beta.step()
    optim_beta.zero_grad()
    optim_f.zero_grad()

    for k in range(10):
        Xn = f(X0)
        KL = ((Xn - X0) ** 2).mean()
        Lf = KL - beta(Xn).mean()
        Lf.backward()
        optim_f.step()
        optim_f.zero_grad()
        optim_beta.zero_grad()

実際に解いてみると以下のようになります．

plt.scatter(X0.cpu()[:,0], X0.cpu()[:,1])
plt.scatter(Y.cpu()[:,0], Y.cpu()[:,1])
plt.scatter(Xn.detach().cpu()[:,0], Xn.detach().cpu()[:,1])

ここで，今回の定式化は最初にやった離散最適輸送とは異なり，今あるサンプルだけでなく新しくサンプリングされた点に対しても，学習後のニューラルネットワークを用いることで輸送先の点を求めることができます．

new_X0 = torch.from_numpy(P0(np.random.rand(50))).float()
new_Xn = f(new_X0.to(device)).detach().cpu().numpy()
new_X0 = new_X0.numpy()

plt.scatter(new_X0[:,0], new_X0[:,1])
plt.scatter(Y.cpu()[:,0], Y.cpu()[:,1])
plt.scatter(new_Xn[:,0], new_Xn[:,1])
plt.plot([new_X0[:,0], new_Xn[:,0]], [new_X0[:,1], new_Xn[:,1]], c="gray", lw=0.5)
plt.show()

エントロピー正則化つき最適輸送

一旦，離散最適輸送に戻って，エントロピー正則化の説明をします． 最適輸送ではよくエントロピー正則化というものを考えます． これは最適輸送の目的関数に以下のような正則化を追加したものとして定式化されます．

$$ \min_{\pi\in \Pi(\mathbb P_0, \mathbb P_1)}\sum_{i=1}^{N_0} \sum_{j=1}^{N_1}\|\boldsymbol x_i - \boldsymbol y_j\|_2^2 \pi_{ij} - \epsilon H(\pi) $$ ここで，$H(\pi)$は$\pi$のエントロピーであり$H(\pi)=-\sum_{i=1}^{N_0}\sum_{j=1}^{N_1}\pi_{ij} (\log \pi_{ij}-1)$です． エントロピー正則化つきの最適輸送では，その名前の通り，輸送計画のエントロピーが大きい解を求めます． エントロピーが大きいとはどういうことかというと，離散最適輸送の場合，各点が少数の点とだけスパースに対応づくのではなく，多くの点とぼやっと対応づくとき，輸送計画のエントロピーが大きくなります． 実際にエントロピー正則化を加えることで輸送計画がどのように変化するのかを見てみます．

X0 = X0.cpu().numpy()
Y = Y.cpu().numpy()
pi = ot.sinkhorn(a,b,((X0[:,None]-Y[None])**2).sum(axis=-1), reg=0.005)

pi = ot.sinkhorn(a,b,((X0[:,None]-Y[None])**2).sum(axis=-1), reg=0.005)
plt.imshow(pi)
plt.show()

plt.scatter(X0[:,0], X0[:,1])
plt.scatter(Y[:,0], Y[:,1])
for i, xi in enumerate(X0):
    for j,yj in enumerate(Y):        
        if pi[i,j] > 0:
            plt.plot((xi[0], yj[0]), (xi[1], yj[1]), c="gray", lw=0.5)

このように，エントロピー正則化の強さ($\epsilon$)を変化させることで，スパースだった対応付けが少しぼやっとしていることがわかります． 対応付がぼやけるということは，ある点を輸送したときに，ある1点に輸送されるのではなく，広がりをもった分布に輸送されることを意味します． これは超解像など，いくつもの正解があり得る不良設定問題をモデル化する上で重要です． ちなみにエントロピー正則化はSinkhorn iterationというGPU上で計算可能なアルゴリズムを使う際によく導入されますが，今回紹介するENOTではSinkhornは関係ありません．

拡散モデル

拡散モデルはデータに徐々にノイズを加えていく拡散過程と，逆にノイズを除去することでデータを生成する逆拡散過程から作られるモデルです． 代表的な拡散モデルであるDDPM[Ho+, 2020]では拡散過程，逆拡散過程が以下のようにモデル化されています． $$ \text{(拡散過程): }\boldsymbol x_{t+1} = \sqrt{\alpha_t}\boldsymbol x_t+\sqrt{1-\alpha_t}\boldsymbol{\epsilon} $$ $$ \text{(逆拡散過程): }\boldsymbol{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t)\right)+ σ_{t} \boldsymbol{z}_t $$ ただし ，$\boldsymbol{z}_t \sim \mathcal N(\boldsymbol{0},\boldsymbol{I})$, $\boldsymbol{\epsilon}\sim \mathcal N(\boldsymbol{0}, \boldsymbol{I})$であり$\alpha_t$は拡散時のノイズの強さを表すパラメータです．

DDPMのような拡散モデルは，時刻が$t=1,2,\ldots, T$と進んでいくという意味で，離散時間拡散モデルと呼ばれます． 一方で，時刻を$t=[0,1]$の連続値として取り扱う拡散モデルも存在します． これを連続時間拡散モデルと呼びます． 連続時間拡散モデルでは拡散過程，逆拡散過程がそれぞれ確率微分方程式として記述されます． 具体的には拡散過程は以下のように記述されます． $$d\boldsymbol{x} = f(\boldsymbol{x}, t)dt + g(t)d\boldsymbol{w}$$ 先程の離散時間拡散モデルは$\boldsymbol x_{t}$から$\boldsymbol x_{t+1}$を求める漸化式として記述されていましたが，連続時間拡散モデルでは微小時間$dt$において，$\boldsymbol x$がどのように変化するのかを表す$d\boldsymbol x$を使って拡散過程を記述しています． ここで，$d\boldsymbol{w}$は標準ウィーナー過程と呼ばれ，微小な間隔$τ$で$\mathcal N(\boldsymbol{0}, τ\boldsymbol{I})$を満たすような乱数です． ウィーナー過程はブラウン運動のモデルとして利用されるものです． $f(t), g(t)$はモデルによって決まる関数を表しています． 例えばDDPMを連続時間に拡張したときは，$d\boldsymbol{x} = -\frac{1}{2}(1-\alpha(t))\boldsymbol{x}dt + \sqrt{1-\alpha(t)}d\boldsymbol{w}$となります．

拡散過程が上記のように書けるとき，逆拡散過程も以下のような確率微分方程式で書くことができます． $$ d\boldsymbol{x} = [f(\boldsymbol{x}, t) - g(t)^2\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x})]dt + g(t)d\bar{{\boldsymbol{w}}} $$ ここで，$\bar{\boldsymbol{w}}$は時間を逆向きにたどったときのウィーナー過程です． ちなみに$\log p_t(\boldsymbol{x})$はスコア関数と呼ばれるものであり，これをニューラルネットワークなどでモデル化することで生成モデルを作るようなもの(スコアベース拡散モデル)も提案されています．

拡散モデルはデータ分布とガウス分布との間の対応関係を求めるモデルとみなすことができます． 図で書くと以下のような感じです． 拡散過程ではデータ分布からガウス分布への(ガタガタの)輸送を行い，逆拡散過程ではガウス分布からデータ分布への輸送を行います． こうやって見ると最適輸送と近そうに見えますが，一方で，拡散モデルと最適輸送の大きな違いとして，拡散モデルでは一方の分布をガウス分布にしなければならないという点があります． これに対して，例えば超解像では低解像度画像の分布と高解像度画像の分布の間の対応関係を求めたいです． 拡散モデルを拡張することで，最適輸送と同様に，任意の分布間の対応付を考えるモデルにすることはできるでしょうか? (ちなみに通常の拡散モデルでも条件付きの生成モデルは考えられており，classifier-free guidanceという方法などがあります．)

シュレディンガー橋

任意の2つの分布間の対応関係を表現するモデルとして，シュレディンガー橋 [Schrödinger, 1931]という最適化問題が知られています． シュレディンガー橋は2つの確率分布$\mathbb P_0, \mathbb P_1$が与えられたとき，以下のような最適化問題として定式化されます． $$ \inf_{T\in \mathcal F(\mathbb P_0, \mathbb P_1)}\text{KL}(T\|W^\epsilon) $$ ここで，$W^\epsilon$: $d\boldsymbol{x} = \sqrt\epsilon d\boldsymbol{w}$はウィーナー過程で，連続時間拡散モデルで出てきた標準ウィーナー過程に$\sqrt \epsilon$をかけたものです． シュレディンガー橋では確率過程$T$を最適化します． また，$\mathcal F(\mathbb P_0, \mathbb P_1)$は$T$を$t=0, 1$で周辺化したときに$\mathbb P_0, \mathbb P_1$になるような制約条件です．

シュレディンガー橋の直感的な意味を説明します(間違ってるかも)． シュレディンガー橋は$\mathbb P_0$から$\mathbb P_1$への輸送経路の分布を最適化する問題であるとみなすことができます． $T$は輸送経路に関する確率分布であるとみなせ，$T$から得られるサンプルはある点をある点に輸送する経路だと思うことができます． シュレディンガー橋では，この経路の分布$T$がウィーナー過程と近くなるようにします． つまり，なるべくブラウン運動っぽい経路をはく分布$T$を求める問題だと思うことができます． ただし，$T$には制約条件があり，ある分布$\mathbb P_0$を$T$から得られる経路で輸送したとき，その輸送した先の分布が$\mathbb P_1$にならなければいけません． ということで，シュレディンガー橋は2つの分布の間をなるべくウィーナー過程っぽい経路でつなぐような最適化問題と思うことができます．

次にシュレディンガー橋を解く方法について説明します． シュレディンガー橋の解は以下の形で書けることが知られています． $$ T_f: d\boldsymbol{x}_t = f(\boldsymbol{x}_t,t )dt + \sqrt{\epsilon}d\boldsymbol{w}, \ \ \mathbb E_{T_f}[\int_0^1 \|f(\boldsymbol{x}_t, t)\|^2 dt] < \infty $$ ここで，確率微分方程式は連続時間の拡散モデルと似た形になっていることがわかります． このとき，シュレディンガー橋は以下の最適化問題になります． $$ \inf_{T_f\in \mathcal D(\mathbb P_0, \mathbb P_1)} \frac{1}{2\epsilon} \mathbb E_{T_f}[\int_0^1 \|f(\boldsymbol{x}_t, t)\|^2dt] $$ ここで，$\mathcal D(\mathbb P_0, \mathbb P_1) \subset \mathcal F(\mathbb P_0, \mathbb P_1)$はエネルギーの条件($\mathbb E_{T_f}[\int_0^1 \|f(\boldsymbol{x}_t, t)\|^2 dt] < \infty$)を満たす$T$の集合を表します． 直感的には，$T$をウィーナー過程+$f$でモデル化したので，$f$の部分を最小化してウィーナー過程っぽい$T$を求めるという最適化問題です． この最適化問題を具体的にどうやって解くのかについては，ENOTの提案部分なので提案法のところで説明します．

ところで，シュレディンガー橋は以下のようにも変形することができます(変形は論文[Gushchin+, 2023]を参照)． $$ \inf_{T\in \mathcal F(\mathbb P_0, \mathbb P_1)}\text{KL}(T \| W^\epsilon) = \inf_{T\in \mathcal F(\mathbb P_0, \mathbb P_1)} \left(\frac{1}{\epsilon}\int_{\mathcal X\times \mathcal Y} \frac{\|x-y\|^2}{2}d\pi^T(x,y) - \epsilon H(\pi^T) + \int_{\mathcal X\times \mathcal Y}\text{KL}(T_{|x,y}\| W_{|x,y}^\epsilon)d\pi^T (x,y)\right) $$ ここで1項目はエントロピー正則化つきの最適輸送そのものです． また，シュレディンガー橋の最適解が求まったとき2項目は0になることが知られています． ということで，シュレディンガー橋を解くことで，エントロピー正則化つきの最適輸送を解くことができます．

ENOT

ではエントロピー正則化つきの最適輸送を解く手法であるENOTについて説明します． 先ほどまでの説明のように，シュレディンガー橋を解くことでエントロピー正則化つきの最適輸送を解くことができます． ENOTではシュレディンガー橋の最適化問題 $$ \inf_{T_f\in \mathcal D(\mathbb P_0, \mathbb P_1)} \frac{1}{2\epsilon} \mathbb E_{T_f}[\int_0^1 \|f(\boldsymbol{x}_t, t)\|^2dt] $$ を解くことで，エントロピー正則化つきの最適輸送を解きます． ENOTでは制約条件をラグランジュの未定乗数法っぽい変形によって緩和し，以下のような最適化問題を考えます． $$\mathcal L(\beta, T_f) = \frac{1}{2\epsilon} \mathbb E_{T_f}[\int_0^1 \|f(\boldsymbol{x}_t, t)\|^2dt] -\int_\mathcal Y \beta(y)d\pi_1^{T_f}(y) + \int_\mathcal Y\beta(y)d\mathbb P_1(y)$$ この式は連続最適輸送のところでやったのと同様に，制約条件を緩和し，ラグランジュ乗数っぽい関数$\beta$を使って制約条件の違反に対してペナルティを課すような最適化問題です． ここで，$\pi_1^{T_f}$は分布$\mathbb P_0$を$T_f$によって輸送(push-forward)したときの分布を表しています． つまり，このペナルティは$\mathbb P_0$を$T_f$によって輸送した分布が$\mathbb P_1$と等しくなるようにするものです． $\mathbb P_0$側の制約条件は式の中では出てきていないですが，これはこのあと説明するアルゴリズムによって自動的に満たされます．

ENOTでは$f$と$\beta$をそれぞれニューラルネットワークによってモデル化し，パラメータを最適化することでこの最適化問題の解を求めます． このとき最適化問題は以下のようになります． $$\sup_\phi \inf_\theta \frac{1}{2\epsilon} \mathbb E_{T_{f_\theta}}[\int_0^1 \|f_\theta(\boldsymbol{x}_t, t)\|^2dt] -\int_\mathcal Y \beta_\phi(y)d\pi_1^{T_{f_\theta}}(y) + \int_\mathcal Y\beta_\phi(y)d\mathbb P_1(y)$$

このロス関数を評価するためには，$T_{f_\theta}$からサンプルを得て，期待値$\mathbb E_{T_{f_\theta}}[\int_0^1 \|f_\theta(\boldsymbol{x}_t, t)\|^2dt]$を評価する必要があります． また，$\mathbb P_0$を輸送した分布$\pi_1^{T_{f_\theta}}$を求め$\int_\mathcal Y \beta_\phi(y)d\pi_1^{T_{f_\theta}}(y)$を評価する必要もあります． これらの値を評価するために，ENOTではEuler-Maruyama simulationを用いて$T_{f_\theta}$からのサンプルを得ます． Euler-Maruyama simulationは以下のように，適当な離散時間幅$\Delta t$を設定したときに，$f$と乱数によって各点がどのように動くのかをシミュレートし，経路を求めるものです．

def euler_maruyama(x0, f, N, epsilon):
    device = x0.device
    B = x0.shape[0]
    D = x0.shape[1]
    dt = 1 / N
    f_hist = []
    xt = x0
    x_hist = [x0.detach().cpu().numpy()]  # TxB
    for t in torch.arange(N, device=device):
        W = torch.randn(B, D).to(device)
        h = torch.cat([xt, t.expand(len(xt), 1)], dim=-1)
        f_t_1 = f(h)  # B
        xt = xt + f_t_1 * dt + (epsilon * dt) ** 0.5 * W
        f_hist.append(f_t_1)
        x_hist.append(xt.detach().cpu().numpy())
    h = torch.cat([xt, t.expand(len(xt), 1)], dim=-1)
    f_t_1 = f(h)
    f_hist.append(f_t_1)

    f_hist = torch.stack(f_hist)
    x_hist = np.array(x_hist)

    return xt, f_hist, x_hist

X0 = torch.from_numpy(X0).float().to(device)
Y =  torch.from_numpy(Y).float().to(device) 
f = lambda h: torch.ones(1).to(device)
Xn,_,X_hist = euler_maruyama(X0, f, N=10, epsilon=0.01)
plt.scatter(X0.cpu()[:,0], X0.cpu()[:,1])
plt.scatter(Xn.detach().cpu()[:,0], Xn.detach().cpu()[:,1], c="C2")
plt.plot(X_hist[:,:,0], X_hist[:,:,1], c="gray", lw=0.5)
plt.show()

では実装したENOTを使って実際にエントロピー正則化つきの最適輸送の解を求めてみます．

epsilon = 0.01
n_hidden = 512
nb_epochs = 2500
N = 10

f = make_net(n_inputs=3, n_outputs=2, n_layers=3, n_hiddens=n_hidden).to(
    device
)
beta = make_net(n_inputs=2, n_outputs=1, n_layers=3, n_hiddens=n_hidden).to(
    device
)
optim_beta = Adam(beta.parameters(), lr=lr)
optim_f = Adam(f.parameters(), lr=lr)

for i in tqdm(range(nb_epochs)):
    Xn, _, _ = euler_maruyama(X0, f, N, epsilon=epsilon)

    Lb = beta(Xn).mean() - beta(Y).mean()
    Lb.backward()
    optim_beta.step()
    optim_beta.zero_grad()
    optim_f.zero_grad()

    for k in range(10):
        Xn, f_hist, X_hist = euler_maruyama(X0, f, N, epsilon=epsilon)

        KL = (f_hist**2).mean()
        Lf = KL - beta(Xn).mean()
        Lf.backward()
        optim_f.step()
        optim_f.zero_grad()
        optim_beta.zero_grad()

plt.scatter(X0.cpu()[:,0], X0.cpu()[:,1])
plt.scatter(Y.cpu()[:,0],  Y.cpu()[:,1])
plt.scatter(Xn.detach().cpu()[:,0], Xn.detach().cpu()[:,1])
plt.plot(X_hist[:,:,0], X_hist[:,:,1], c="gray", lw=0.5)
plt.show()

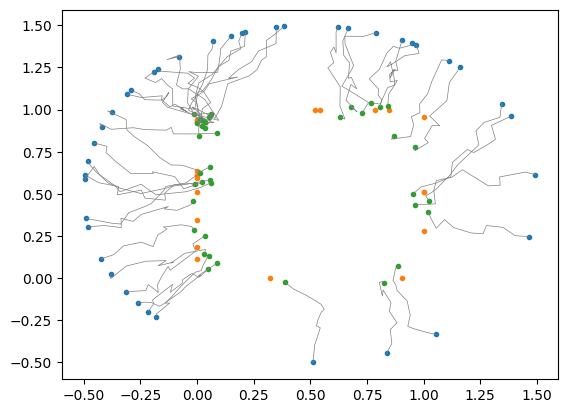
終わりに

今回は自分の理解のためにENOTの実装を行いました． 提案法はシュレディンガー橋とエントロピー正則化つきの最適輸送の関係を利用することで，ニューラルネットワークを使って最適輸送を解く方法でした． 実装をしてみた感触としては，最適化があまり安定してないような予感がありました． ロス関数は，$\beta$をdiscriminatorとみなすとGANのような定式化だと思うことができ，あまり安定しなくてもしょうがないのかもという気がします． 今回実装したENOT以外にもシュレディンガー橋を解く方法はいくつか提案されているようなので，引き続き勉強してそのあたりの手法も実装してみたいと思っています．

参考