Stanで気温変動のフィッティング
はじめに
この記事は Stan Advent Calendar 2016のn日目の記事ではありません。
21日目の記事です。
話題のアヒル本(言われるまで何がアヒルなのかわからなかった)を読んだ。
Stanの文法を知るために買ったけれど、全体的に統計モデリング、解析について書いてあって、勉強になった。 本を読んで勉強になったことはたくさんあるけど、特にグラフを死ぬほど書かないといけないという認識を持った。 自分ではそれなりにグラフを書いているつもりだったけれど、pariplotとかviolinplotとかちゃんと書いたことがなかった。
せっかく本を読んだので、適当にデータをとってきて解析してAdvent Calendarなるものに挑戦しようと思っていたけど、もう埋まっていた。悲しいので一人で勝手にやることにする。
よく見たら21日が空いていたので、フライングということにさせてください。
今回は特に12章を見ながら時系列データをいじくることにした。
知識がないので、間違ったことをしていたら教えていただけると嬉しいです。
データ
時系列データとして天気に関するデータを使うことにした。 気象庁のサイト から天気に関するいろんなデータがダウンロードできるので利用する。
今回は愛知県の気温とか降水量とかを過去5年分ぐらいダウンロードした。 日本語のファイルがやや面倒だった。
import pandas as pd aichi = pd.read_csv("./weather_aichi.csv", encoding='SHIFT-JIS') aichi["年"] = aichi[u"年月日"].apply(lambda x: x.split("/")[0]) aichi["月_s"] = aichi[u"年月日"].apply(lambda x: "%02d"%int(x.split("/")[1])) aichi["日_s"] = aichi[u"年月日"].apply(lambda x: "%02d"%int(x.split("/")[2])) aichi["m"] = aichi[u"年月日"].apply(lambda x: int(x.split("/")[1])) aichi["d"] = aichi[u"年月日"].apply(lambda x: int(x.split("/")[2])) aichi["is_rain"] = aichi[u"降水量の合計(mm)"]>0 aichi = aichi.set_index(u"年月日") month_groups = aichi.groupby("月_s") aichi
| Unnamed: 0 | 平均気温(℃) | 降水量の合計(mm) | 年 | 月_s | 日_s | m | d | is_rain | |
|---|---|---|---|---|---|---|---|---|---|
| 年月日 | |||||||||
| 2011/12/3 | 1 | 12.2 | 8.5 | 2011 | 12 | 03 | 12 | 3 | True |
| 2011/12/4 | 2 | 11.9 | 0.0 | 2011 | 12 | 04 | 12 | 4 | False |
| 2011/12/5 | 3 | 10.4 | 0.0 | 2011 | 12 | 05 | 12 | 5 | False |
| 2011/12/6 | 4 | 8.0 | 0.5 | 2011 | 12 | 06 | 12 | 6 | True |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2016/11/30 | 1825 | 8.2 | 0.0 | 2016 | 11 | 30 | 11 | 30 | False |
| 2016/12/1 | 1826 | 12.0 | 0.0 | 2016 | 12 | 01 | 12 | 1 | False |
| 2016/12/2 | 1827 | 11.0 | 0.0 | 2016 | 12 | 02 | 12 | 2 | False |
| 2016/12/3 | 1828 | 9.8 | 0.0 | 2016 | 12 | 03 | 12 | 3 | False |
1828 rows × 9 columns
今回は、平均気温をモデリングしてみることにした。 とりあえずグラフを書く。
%matplotlib inline import pylab as plt import seaborn as sns import matplotlib.font_manager as fm font = {'family' : 'TakaoGothic'} plt.rc('font', **font) ax = aichi[[ u"平均気温(℃)"]].plot(figsize=(20,10))
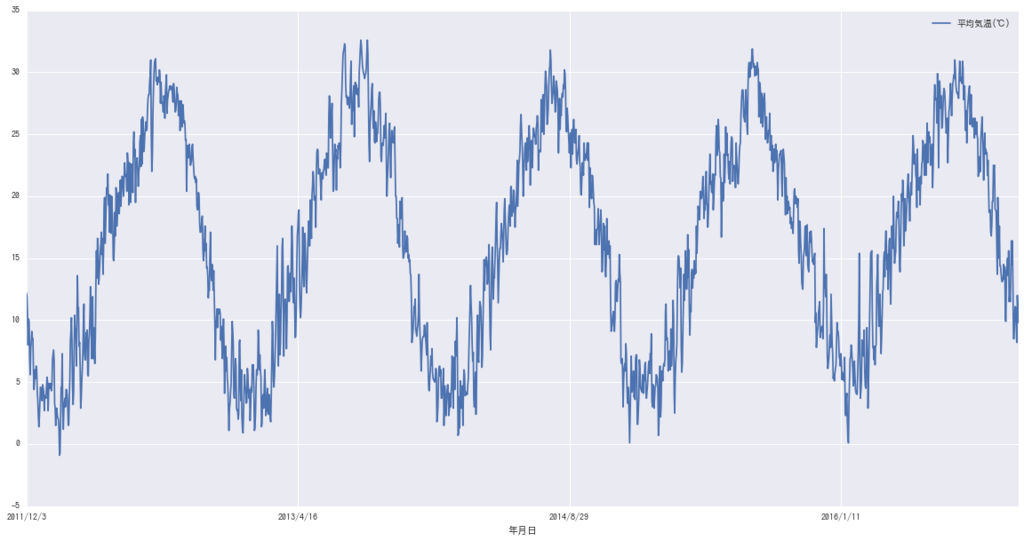
当たり前だけど春夏秋冬がある。 雨のデータも後で使うのでプロットする。
ax = aichi[ u"平均気温(℃)"]["2011/12/3": "2012/12/3"].plot(figsize=(20,10)) aichi[ u"降水量の合計(mm)"]["2011/12/3": "2012/12/3"].plot( kind="bar", ax=ax) plt.show()
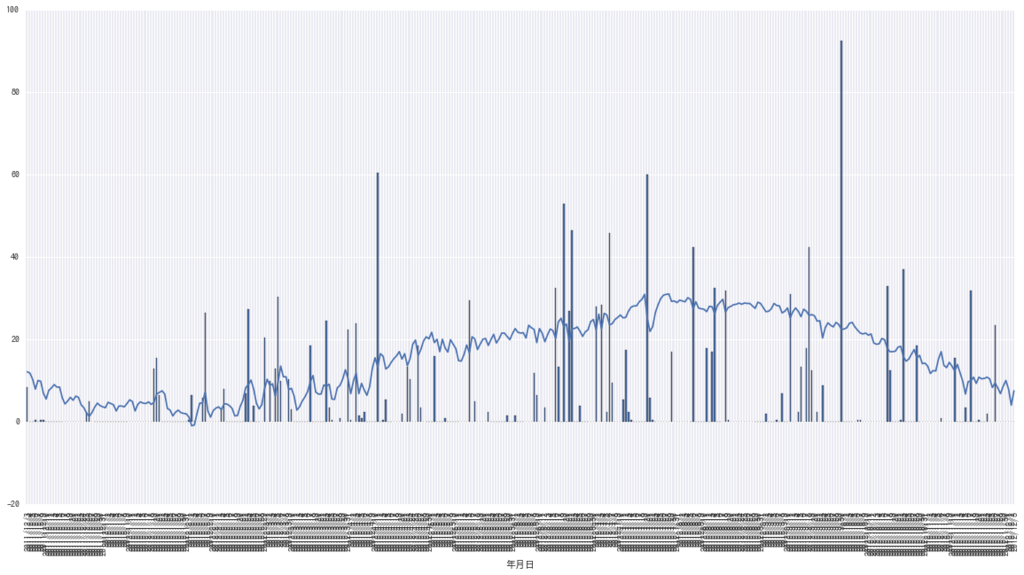
その他色々プロットを書く。
sns.pairplot(aichi[[u"平均気温(℃)", u"降水量の合計(mm)", "m"]], hue="m", size=4)
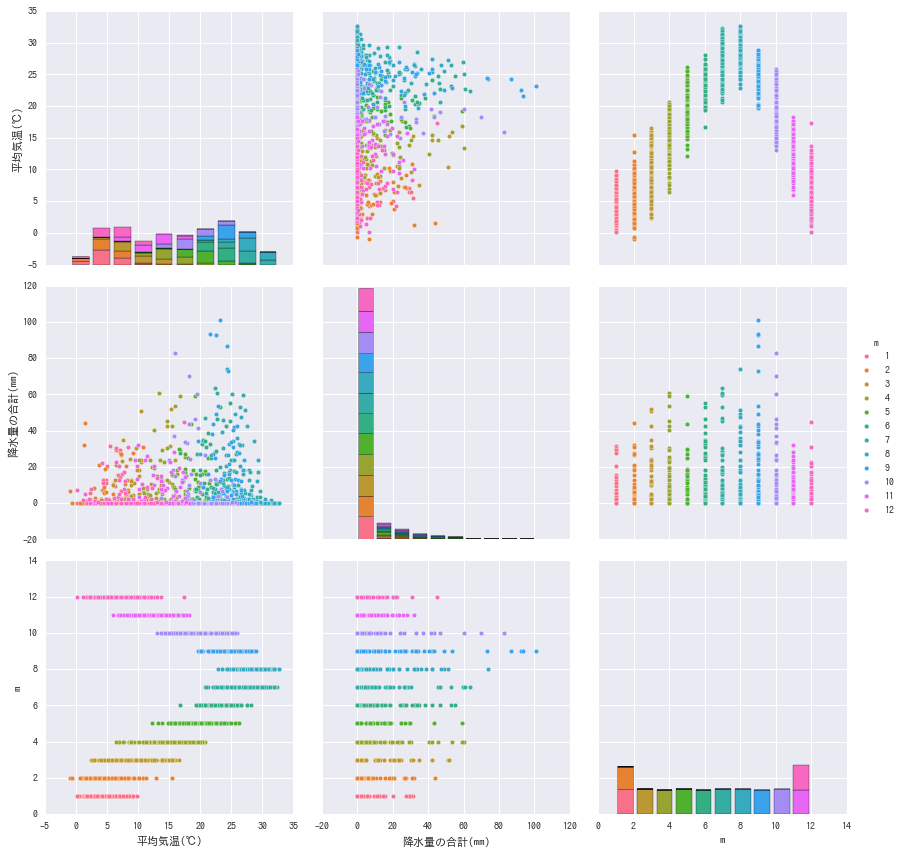
アヒル本では対角線の上と下で別のプロットを書いていたけど、正直手でやるのはちょっと面倒。 変数の型とか見て自動でやるやつをそのうち作りたい。
fig, ax = plt.subplots(figsize=(20,20)) sns.violinplot(data=aichi, x="m", y =u"平均気温(℃)") fig, ax = plt.subplots(figsize=(20,20)) sns.violinplot(data=aichi, x="m", y =u"平均気温(℃)", hue="is_rain", split=True) plt.show()
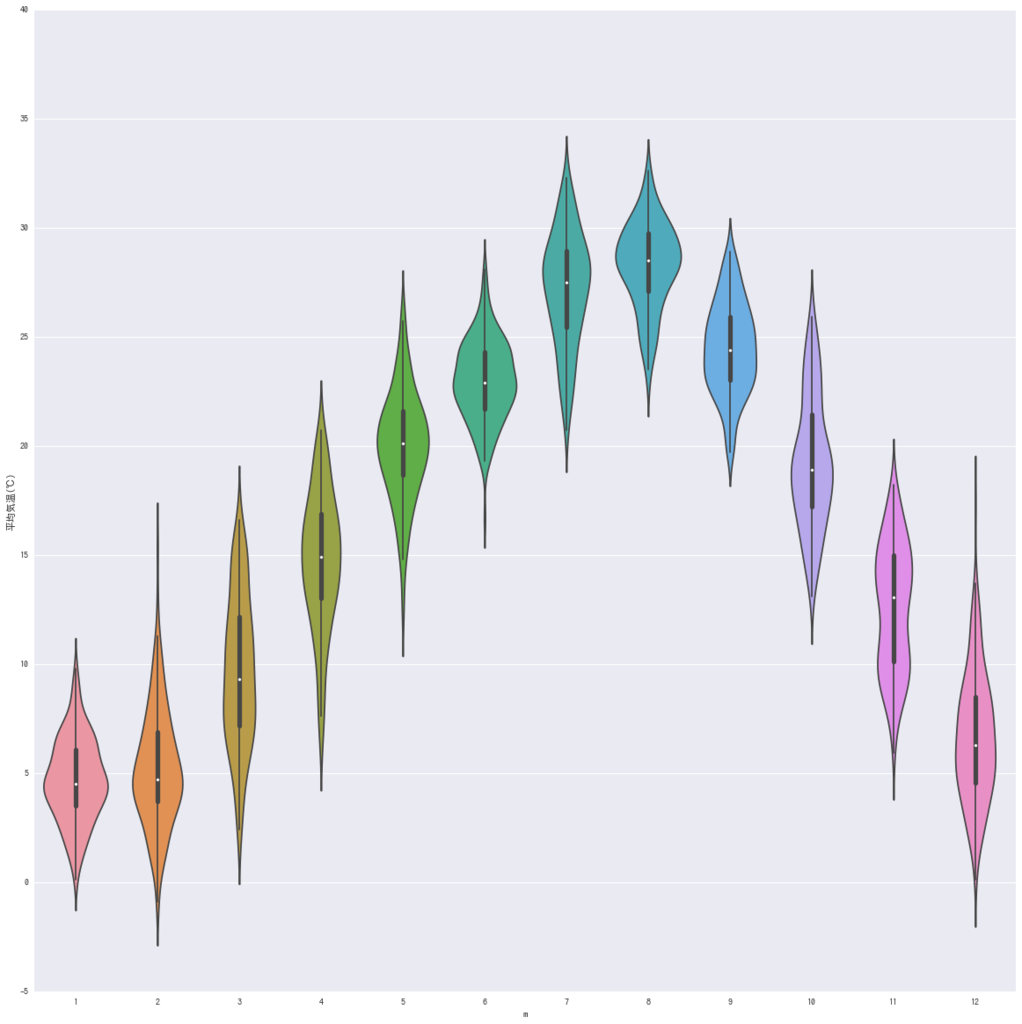
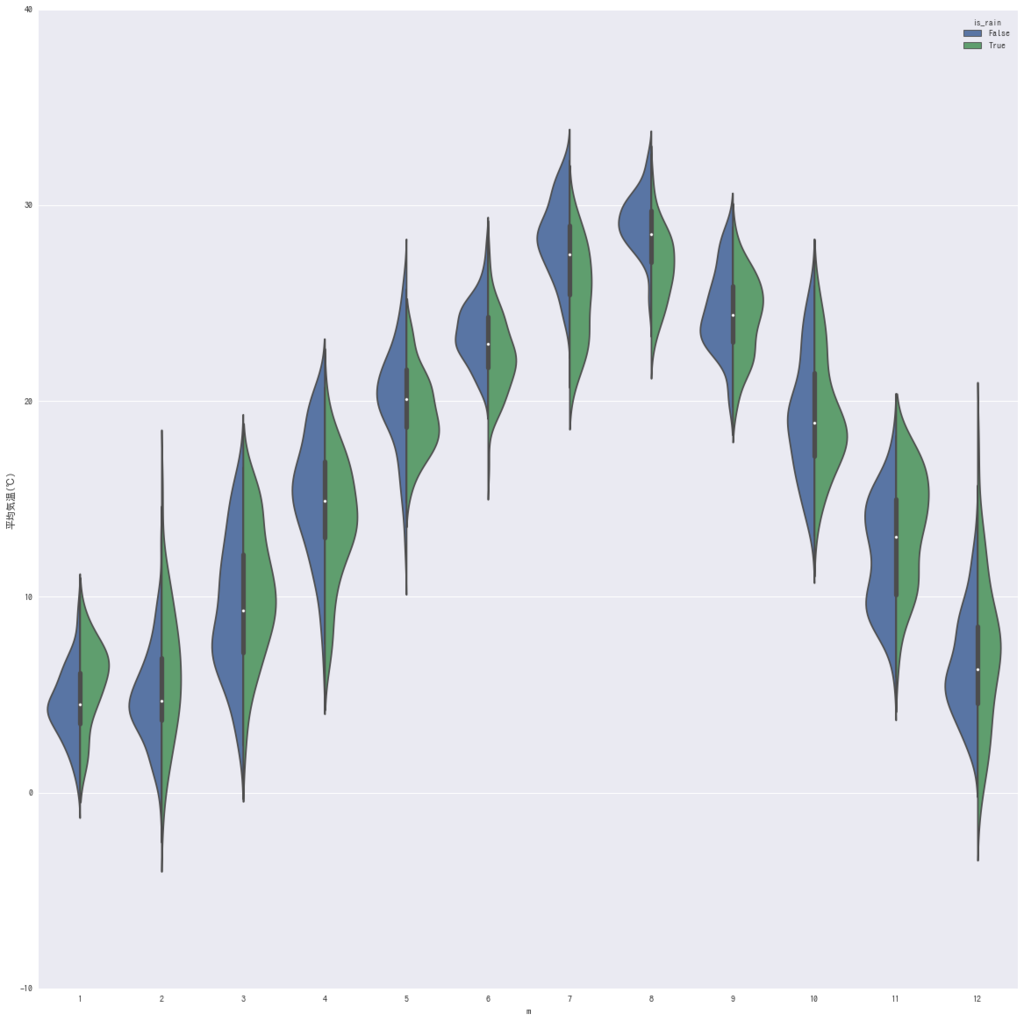
雨が降ると夏は気温が下がるけど、冬は逆に気温が高い。そりゃそうだな。
temperatures = aichi[u"平均気温(℃)"].get_values() data = {"Y":temperatures, "N":len(aichi), "is_rain":aichi["is_rain"].astype(int).get_values()+1}
状態空間モデルでのフィッティング
アヒル本12章を見ながら、いくつかのモデルを使って気温の変動をモデル化する。
状態空間モデル(1階差分)
観測された気温()は
真の気温(
)を平均とする正規分布に従い、
真の気温は、前日の真の気温を平均とする正規分布に従うというモデルを仮定する。
式的には以下。
以下のようにStanでモデルを書ける。
data{
int N;
vector[N] Y;
}
parameters{
vector[N] mu;
real<lower=0> s_mu;
real<lower=0> s_Y;
}
model{
mu[2:N] ~ normal(mu[1:(N-1)], s_mu);
Y ~ normal(mu, s_Y);
}
python からStanをよんでサンプリングして、色々とプロットする。
import pystan import numpy as np def fit(model_filename): fit = pystan.stan(model_filename, data=data) ms = fit.extract() fit.plot() return fit, ms def fit_plot(fit, ms, list_max_x=[-1,500,100,50], ylim=None): mu_mean = ms["mu"].mean(axis=0) mu_std = ms["mu"].std(axis=0) def plot_line(max_x): fig = plt.figure(figsize=(10,10)) plt.plot(mu_mean[:max_x], linewidth=0.5) plt.scatter(range(len(temperatures[:max_x])), temperatures[:max_x], marker=".",# linestyle="None", c=aichi["is_rain"].get_values()[:max_x].astype(float)) plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std)[:max_x], (mu_mean+mu_std)[:max_x], alpha=0.3) plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std*2)[:max_x], (mu_mean+mu_std*2)[:max_x], alpha=0.2) plt.xlim(0, len(temperatures[:max_x])) if not ylim==None: plt.ylim(*ylim) plt.show() for max_x in list_max_x: plot_line(max_x)
fit1 = fit("./model.stan") fit_plot(*fit1, list_max_x=[-1,100])
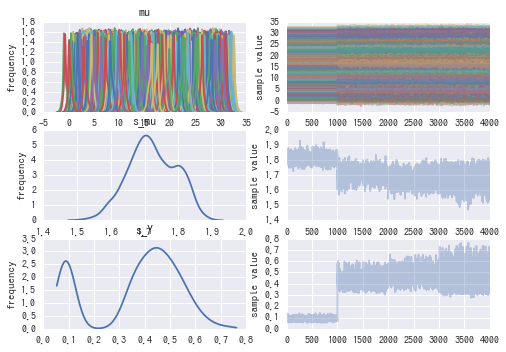
1000のあたりとか、見るからにサンプリングが安定していない感じがある。 サンプリング結果を見てみる。
fit1[0]
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu[0] 12.18 6.1e-3 0.39 11.34 11.99 12.19 12.36 12.98 4000.0 1.0 mu[1] 11.84 6.0e-3 0.38 10.98 11.66 11.87 12.04 12.63 4000.0 1.0 mu[2] 10.36 6.1e-3 0.38 9.49 10.16 10.39 10.54 11.15 4000.0 1.0 mu[3] 8.21 6.5e-3 0.41 7.47 7.96 8.12 8.46 9.13 4000.0 1.05 mu[4] 9.99 6.2e-3 0.39 9.1 9.77 10.04 10.2 10.74 4000.0 1.02 mu[1825] 11.77 6.5e-3 0.41 10.85 11.53 11.87 12.04 12.48 4000.0 1.07 mu[1826] 10.97 6.1e-3 0.39 10.14 10.78 10.99 11.18 11.76 4000.0 1.0 mu[1827] 9.86 6.3e-3 0.4 9.08 9.67 9.83 10.06 10.75 4000.0 1.0 s_mu 1.72 0.04 0.07 1.59 1.67 1.72 1.78 1.85 3.0 1.71 s_Y 0.37 0.12 0.18 0.07 0.2 0.42 0.49 0.63 2.0 3.15 lp__ -622.4 903.47 1277.7 -1830 -1483 -1218 121.56 1970.3 2.0 5.28
アヒル本によると、
とあるので、今回のサンプリングではs_muやs_Yはまともにサンプリングされていないことがわかる。
また、Rhatはパラメータが収束したかどうかを表す値であり、
「chain数が3以上ですべてのパラメータでRhat < 1.1 となること」を「収束した」と見なすことにする。
とある。 ということで、このモデルではうまく収束しなかった。 サンプリング数を増やしたりしてもいいのかもしれないが、今回は別のモデルを作ることにする。
状態空間モデル(2階差分)
真の気温の変化はその前の日の真の気温の変化を平均とする正規分布に従うというモデル。 式的には以下。
Stanのコードは以下。
data{
int N;
vector[N] Y;
}
parameters{
vector[N] mu;
real<lower=0> s_mu;
real<lower=0> s_Y;
}
model{
mu[3:N] ~ normal(2 * mu[2:(N-1)] - mu[1:(N-2)], s_mu);
Y ~ normal(mu, s_Y);
}
サンプリングする。
fit2 = fit("./model2.stan") fit_plot(*fit2, list_max_x=[-1,100])
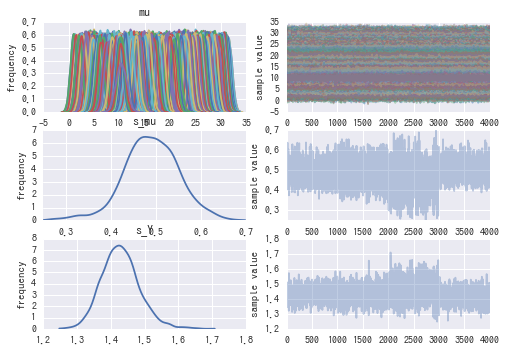
サンプリング結果
fit2[0]
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu[0] 12.12 0.02 1.06 10.07 11.42 12.13 12.83 14.17 4000.0 1.0 mu[1] 11.26 0.01 0.76 9.76 10.75 11.25 11.78 12.75 4000.0 1.0 mu[2] 10.41 0.01 0.67 9.12 9.95 10.41 10.86 11.73 4000.0 1.0 mu[3] 9.64 0.01 0.68 8.28 9.19 9.65 10.09 10.97 4000.0 1.0 mu[4] 9.04 0.01 0.68 7.7 8.59 9.04 9.49 10.38 4000.0 1.0 mu[1825] 10.28 0.01 0.67 8.99 9.82 10.28 10.73 11.59 4000.0 1.0 mu[1826] 10.4 0.01 0.75 8.94 9.9 10.38 10.9 11.89 4000.0 1.0 mu[1827] 10.42 0.02 1.04 8.42 9.72 10.42 11.14 12.39 4000.0 1.0 s_mu 0.49 9.5e-3 0.06 0.35 0.45 0.49 0.53 0.61 42.0 1.1 s_Y 1.43 7.5e-3 0.06 1.33 1.39 1.43 1.46 1.55 55.0 1.07 lp__ -1158 28.55 180.58 -1459 -1281 -1171 -1060 -711.0 40.0 1.09
Rhatの値を見てみる1.1ギリギリという感じ。 n_effも50とかしかないので、厳しそう。
一応のベイズ信頼区間のグラフを見る。
白丸が晴れの日、黒丸は雨の日を表す。
濃い青は68%ぐらい、薄い青は95%ぐらい。
青線は平均値を表す。
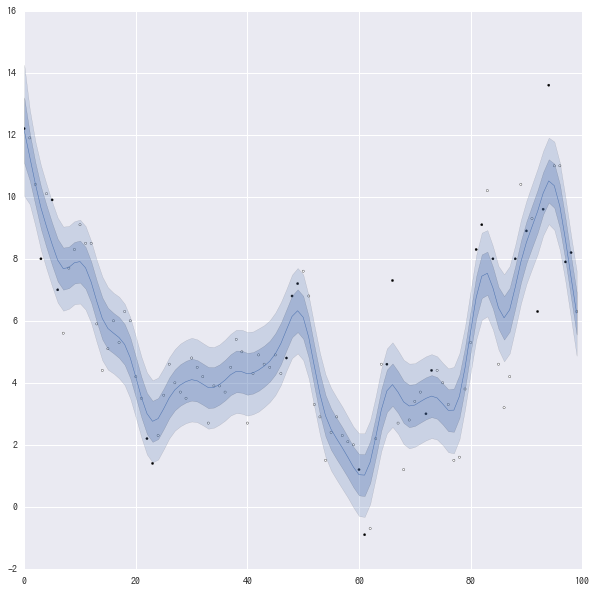
なんとなく雨の日が上手くあっていないような気がする。 雨が降ると前日との温度差が大きくなることが予想されるので、そのへんのモデルをちゃんと作ったほうが良さそう。
状態空間モデル(2階差分 降水量を考慮するモデル)
はじめの方に描いたグラフなどから天気を考慮する必要がありそう。 そこで、この題材に対するモチベーションとモデルの当てはまりから以下のようなモデルを仮定する。
雨のとき
雨がふらなかったとき
雨が振った日と振らなかった日では、真の気温から観測値へ乱数の分散が変わるというモデル 本当は分散だけでなく平均も変わったほうがいい気がするが、その変わり方が季節ごとに違うので面倒でやめた。
fit3 = fit("./model3.stan") fit_plot(*fit3, list_max_x=[-1,100])
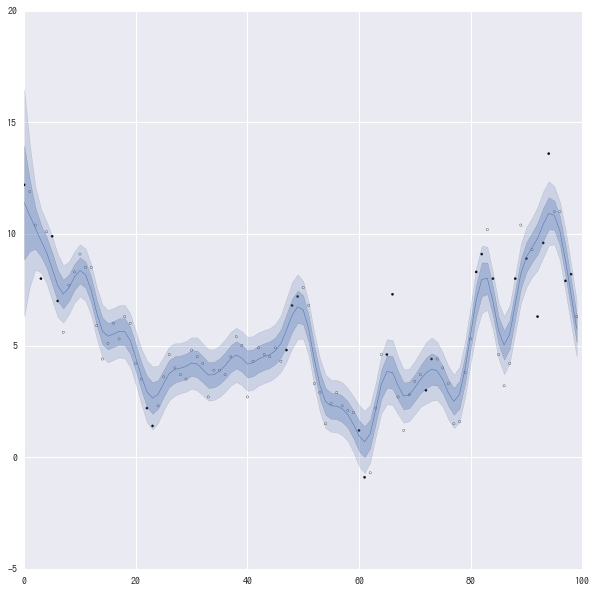
fit3[0]
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu[0] 11.41 0.04 2.55 6.51 9.72 11.38 13.13 16.4 4000.0 1.0 mu[1] 10.83 0.03 1.59 7.72 9.74 10.84 11.9 13.97 4000.0 1.0 mu[2] 10.26 0.01 0.93 8.46 9.64 10.25 10.89 12.09 4000.0 1.0 mu[3] 9.71 0.01 0.72 8.32 9.22 9.7 10.18 11.11 4000.0 1.0 mu[1826] 10.52 9.9e-3 0.63 9.31 10.08 10.52 10.96 11.77 4000.0 1.0 mu[1827] 10.38 0.01 0.88 8.65 9.78 10.39 10.99 12.07 4000.0 1.0 s_mu 0.69 7.5e-3 0.07 0.55 0.64 0.69 0.74 0.82 88.0 1.03 s_Y[0] 1.06 5.5e-3 0.06 0.95 1.01 1.05 1.1 1.18 123.0 1.02 s_Y[1] 1.7 2.9e-3 0.07 1.57 1.65 1.7 1.75 1.84 583.0 1.01 lp__ -1508 13.2 122.38 -1712 -1595 -1520 -1433 -1247 86.0 1.03
前のモデルよりちゃんと収束してる感はある。 s_Y[1]が雨が降った日なので、雨の日は晴れの日よりも、真の気温からの分散が大きくなる。
前のモデルとの違いがぱっとわからないので、重ねてグラフをかく。
fig = plt.figure(figsize=(10,10)) max_x = 100 colors = ["b", "g"] for i,ms in enumerate([fit2[1], fit3[1]]): mu_mean = ms["mu"].mean(axis=0) mu_std = ms["mu"].std(axis=0) plt.plot(mu_mean[:max_x], linewidth=0.5) plt.scatter(range(len(temperatures[:max_x])), temperatures[:max_x], marker=".",# linestyle="None", c=aichi["is_rain"].get_values()[:max_x].astype(float)) #plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std)[:max_x], (mu_mean+mu_std)[:max_x], alpha=0.3) plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std*2)[:max_x], (mu_mean+mu_std*2)[:max_x], alpha=0.2 ,color=colors[i]) plt.xlim(0, len(temperatures[:max_x])) plt.ylim([-5, 20]) plt.show()
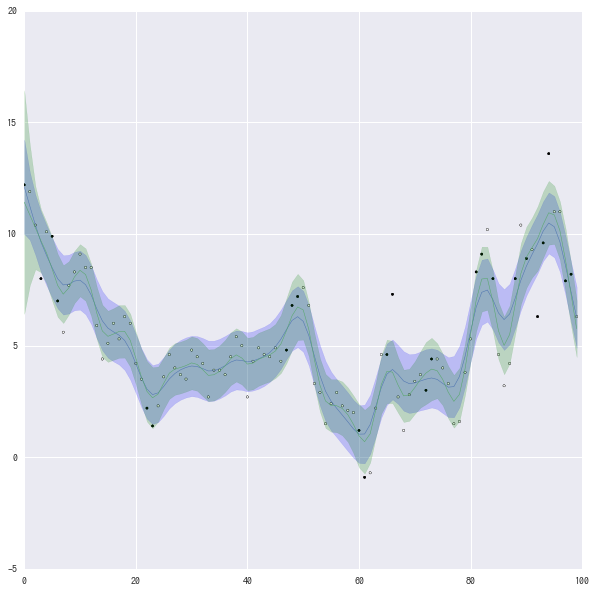
青が単純な2階差分、緑が雨で条件わけしたモデル。 正直良くなっているのかどうかよくわからない。
まとめと今後
アヒル本を参考にして、気温変動のモデリングを行った。 Stanの使い方はなんとなくわかってきたけど、 統計的に正しいのかとか、いまいちよくわかっていない。
今回は年ごとの関係を考慮しないでモデルを作った。 sinとかでモデル化できそうな気がする。 また、雨の日と晴れの日でsinの強さが変わるようにすると、もっといい感じにモデル化できるように思う。
Stanでまだわかってないことの1つにディリクレ混合過程がある。 アヒル本には載っていなかったけど、このへんを見ながらやってみたい。
fit.plot()のfig_sizeを大きくしたいんだけど、どうやらpython側でなくstan側からプロットされている(?)ようで、いまいちやり方がわからなかった。
(この記事には、グラフを死ぬほどかかないといけないという認識があまり反映されていないのではないか。)