この記事はJulia Advent Calendar 2017の17日目の記事です.
普段はpythonばかり書いていて,juliaは最近文法覚えてきたかなレベルなので色々許してください.
コードの全体はここにあります.
概要
- この記事では擬似コードや数式を可能な限りそのままプログラムすることを目的とします.
- unicode文字を使いまくって以下の画像のようなプログラムを作成します.
- juliaとpythonで実装して,書きやすさと実行速度を比較します.
- 書きやすさが悪化するので型指定はしません.
- 結論は以下です.
- juliaのほうが色んなunicode文字が使えるから,書きやすく可読性が高い.
- インデックスが1から始まるのがいい.
- juliaのほうが倍程度速くなることもあるけど,思ったより速くならない (型指定してないから)
- juliaのeinsumを何も考えずに使うと激遅になる.(僕がやらかしてるかも)
unicode文字は以下の埋め込みではおそらく微妙な感じに表示されますが,ちゃんと設定されたエディタやjupyter notebookでは以下のように表示されます.
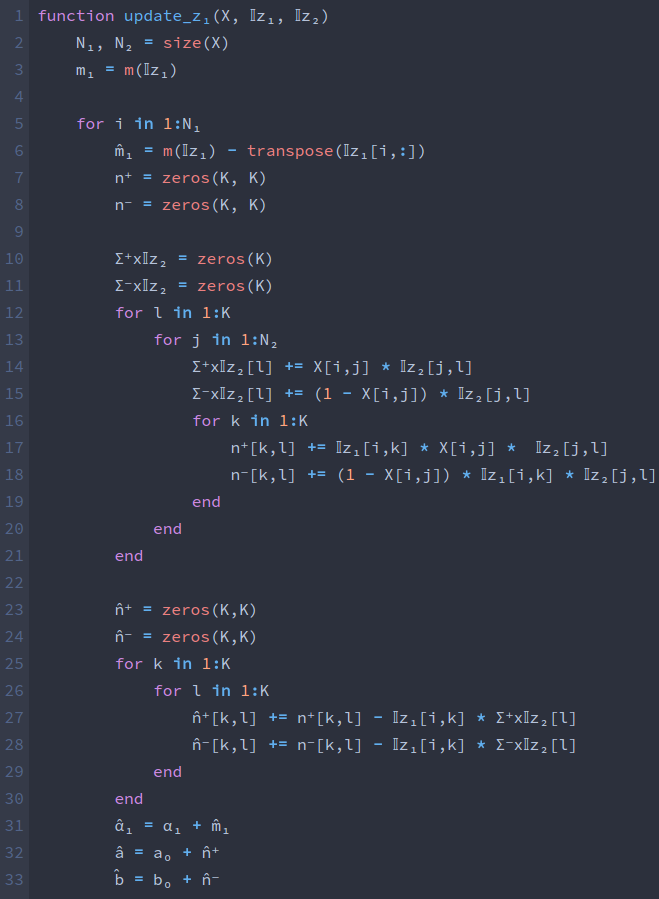
Table of Contents
はじめに (式or擬似コードに可能な限り近いプログラム)
数式を見て実装するときや論文に書いてある擬似コードを実装するとき,可能な限りそれらに近いプログラムを書くようにしている.
数式/擬似コードとプログラムを近づけるために,などunicode文字を多用する.
このようなプログラムを書くことで,
という利点がある.
例えばNo-U-Turn Sampler Hoffman+, 2011の擬似コード(の一部,論文より引用)は

これに対して書いたpythonコードは以下.
def BuildTree(θ, r, u, v, j, ε): if j == 0: θd, rd = Leapfrog(x, θ, r, v * ε) if np.log(u) <= (L(*θd) - 0.5 * np.dot(rd, rd)): Cd_ = [[θd, rd]] else: Cd_ = [] sd = int(np.log(u) < (Δ_max + L(*θd) - 0.5 * np.dot(rd, rd))) return θd, rd, θd, rd, Cd_, sd else: θ_minus, r_minus, θ_plus, r_plus, Cd_, sd = BuildTree(θ, r, u, v, j - 1, ε) if v == -1: θ_minus, r_minus, _, _, Cdd_, sdd = BuildTree(θ_minus, r_minus, u, v, j - 1, ε) else: _, _, θ_plus, r_plus, Cdd_, sdd = BuildTree(θ_plus, r_plus, u, v, j - 1, ε) sd = sdd * sd * int((np.dot(θ_plus - θ_minus, r_minus) >= 0) and (np.dot(θ_plus - θ_minus, r_plus) >= 0)) Cd_.extend(Cdd_) return θ_minus, r_minus, θ_plus, r_plus, Cd_, sd
pythonではギリシャ文字などの一部のunicode文字を変数に使うことができる.
しかし,一部の例えば
や
などの記号は使うことができないため,微妙に見難い感じになってしまっていた.
探してみるとjuliaで同じことをしている人がいて,こちらのほうがだいぶ良さそうだった.
juliaでは↑であげたような文字に加えて
みたいな修飾文字や不等号の
とかを使える.
juliaで使えるunicode文字一覧はこちら.
juliaすごい.ということで,以下ではこれまでpythonで実装したコードをjuliaで書きなおし,書きやすさと実行速度を比較する.
NUTSは既にやられているようなので
- Dynamic Time Warping
- Stochastic Block Model
について実装する.
juliaは型をちゃんと指定するともっと速くなるが,「そのまま実装する」という目的に反するのでやらない.
ちなみにNUTSのpython実装の話はこっち.
Dynamic Time Warping
Dynamic Time Warping (DTW) は,2つの連続値系列データのいい感じの距離を求めるアルゴリズム. 動的計画法で解く. pythonで実装したときの記事はこっち ksknw.hatenablog.com
A global averaging method for dynamic time warping, with applications to clustering (DTW自体の論文ではない) の擬似コードを参考にしてプログラムを書く. 擬似コードは以下.


(ただしこの擬似コードは多分間違っているので,m[i,j]の遷移前のインデックスをsecondに入れるように変えた.)
python
δ = lambda a,b: (a - b)**2 first = lambda x: x[0] second = lambda x: x[1] def minVal(v1, v2, v3): if first(v1) <= min(first(v2), first(v3)): return v1, 0 elif first(v2) <= first(v3): return v2, 1 else: return v3, 2 def dtw(A, B): S = len(A) T = len(B) m = [[0 for j in range(T)] for i in range(S)] m[0][0] = (δ(A[0],B[0]), (-1,-1)) for i in range(1,S): m[i][0] = (m[i-1][0][0] + δ(A[i], B[0]), (i-1,0)) for j in range(1,T): m[0][j] = (m[0][j-1][0] + δ(A[0], B[j]), (0,j-1)) for i in range(1,S): for j in range(1,T): minimum, index = minVal(m[i-1][j], m[i][j-1], m[i-1][j-1]) indexes = [(i-1,j), (i,j-1), (i-1,j-1)] m[i][j] = (first(minimum)+δ(A[i], B[j]), indexes[index]) return m
擬似コードや数式ではインデックスを1から始めることが多いが,pythonは0からなので,頭の中でインデックスをずらしながらプログラムを書く必要がある. 他にはv1が添字っぽくない程度で,大体そのまま書けた.
julia
δ(a,b) = (a - b)^2 # first(x) = x[1] firstは元からあるのでいらない second(x) = x[2] function minVal(v₁, v₂, v₃) if first(v₁) ≤ minimum([first(v₂), first(v₃)]) return v₁, 1 elseif first(v₂) ≤ first(v₃) return v₂, 2 else return v₃, 3 end end function DTW(A, B) S = length(A) T = length(B) m = Matrix(S, T) m[1, 1] = [δ(A[1], B[1]), (0,0)] for i in 2:S m[i,1] = [m[i-1, 1][1] + δ(A[i], B[1]), [i-1, 1]] end for j in 2:T m[1,j] = [m[1, j-1][1] + δ(A[1], B[j]), [1, j-1]] end for i in 2:S for j in 2:T min, index = minVal(m[i-1,j], m[i,j-1], m[i-1,j-1]) indexes = [[i-1, j], [i, j-1], [i-1, j-1]] m[i,j] = first(min) + δ(A[i],B[j]), indexes[index] end end return m end
endがある分pythonより長い.一方でpythonでは使えない
とか
が使えるので,より忠実な感じになっている.
実際に書いてみるとわかるけど,インデックスが擬似コードと同じなのは結構大事で,全然頭を使わずにそのまま書けた.
実行速度比較
juliaはpythonに比べて速いらしいので実行速度を比較した. シェルのtime を使って実行速度を比較した. コードの全体はここにある.
julia dtw_julia.jl 2.62s user 0.30s system 110% cpu 2.641 total python dtw_python.py 2.76s user 0.11s system 99% cpu 2.873 total
期待していたよりも全然速くならなかった. 実行時間が短くてコンパイルのオーバヘッドが大きいのかなと思ったから,forで10回実行するようにした結果が以下.
julia dtw_julia.jl 21.97s user 0.66s system 101% cpu 22.355 total python dtw_python.py 25.81s user 0.78s system 99% cpu 26.591 total
多少速い気がするけど,期待としては数十倍とかだったので,いまいち. 型指定していないとこれぐらいなのかな(?)
Stochastic Block Model
Stochastic Block Model (SBM)は非対称関係データのクラスタリング手法.
隠れ変数の事後分布をサンプリングして近似する(周辺化ギブスサンプラー).
今回の例では特にクラスタ割り当て
の事後分布を求めて,サンプリングする部分をやる.
pythonでの実装したときの記事はこっち. ksknw.hatenablog.com
関係データ学習という本に載っているクラスタzの事後確率に関する数式は以下.
,
をサンプリングする。
他の変数がgivenだとした時の、の事後確率は、
ここで、
はガンマ関数で、
はパラメータ
この事後分布を求めてサンプリングする部分をpythonとjuliaで比較する. 全部書くと見づらいので一部だけ,コードの全体は同じくここにある.
python
n_pos = np.einsum("ikjl, ij", np.tensordot(z1, z2, axes=0), X) # n_pos_kl = n_pos[k][l] n_neg = np.einsum("ikjl, ij", np.tensordot(z1, z2, axes=0), 1 - X) m1_hat = lambda i: m1 - z1[i] # m1_hat_k = m1_hat[k] n_pos_hat = lambda i: n_pos - np.einsum("kjl, j", np.tensordot(z1, z2, axes=0)[i], X[i]) n_neg_hat = lambda i: n_neg - np.einsum("kjl, j", np.tensordot(z1, z2, axes=0)[i], 1 - X[i]) α_1_hat = lambda i: α1 + m1_hat(i) a_hat = lambda i: a0 + n_pos_hat(i) b_hat = lambda i: b0 + n_neg_hat(i) aᵢhat = a_hat(i) bᵢhat = b_hat(i) p_z1ᵢ_left = logΓ(aᵢhat + bᵢhat) - logΓ(aᵢhat) - logΓ(bᵢhat) p_z1ᵢ_right_upper = logΓ(aᵢhat + np.dot(X[i], z2)) + logΓ(bᵢhat + np.dot((1 - X[i]), z2)) p_z1ᵢ_right_lower = logΓ(aᵢhat + bᵢhat + m2) p_z1ᵢ = (α_1_hat(i) * exp(p_z1ᵢ_left + p_z1ᵢ_right_upper - p_z1ᵢ_right_lower)).prod(axis=1) p_z1ᵢ = p_z1ᵢ.real p_z1ᵢ = p_z1ᵢ / p_z1ᵢ.sum() new_z1.append(onehot(choice(range(nb_k), p=p_z1ᵢ), nb_k))
数式には
や
などが頻出するが,pythonではこれらの文字を使うことができない.
このため,m1_hatやn_posなどの変数名になってしまっている.
julia
@einsum n⁺[k,l] := X[i,j] * 𝕀z₁[i,k] * 𝕀z₂[j,l] @einsum n⁻[k,l] := (ones(X)[i,j] - X[i,j]) * 𝕀z₁[i,k] * 𝕀z₂[j,l] m̂₁ = m(𝕀z₁) - transpose(𝕀z₁[i,:]) @einsum Σ⁺x𝕀z₂[i,l] := X[i,j] * 𝕀z₂[j,l] @einsum Σ⁻x𝕀z₂[i,l] := (ones(X)[i,j] - X[i,j]) * 𝕀z₂[j,l] @einsum n̂⁺[k,l] := n⁺[k,l] - 𝕀z₁[i,k] * Σ⁺x𝕀z₂[i,l] @einsum n̂⁻[k,l] := n⁻[k,l] - 𝕀z₁[i,k] * Σ⁻x𝕀z₂[i,l] α̂₁ = α₁ + m̂₁ â = a₀ + n̂⁺ b̂ = b₀ + n̂⁻ temp⁺ = zeros(â) temp⁻ = zeros(â) temp = zeros(â) for j in 1:size(temp⁺)[1] temp⁺[j,:] = Σ⁺x𝕀z₂[i,:] temp⁻[j,:] = Σ⁻x𝕀z₂[i,:] temp[j,:] = sum(𝕀z₂,1) end @einsum p_z₁[k,l] := exp(logΓ(â + b̂)-logΓ(â)-logΓ(b̂) + logΓ(â+temp⁺)+logΓ(b̂+temp⁻)-logΓ(â+b̂+temp))[k,l] p_z₁ = α̂₁ .* transpose(prod(p_z₁, 2)) p_z₁ /= sum(p_z₁) 𝕀z₁[i,:] = onehot(sample(1:K, Weights(p_z₁[:])), K)
pythonに対してjuliaではα̂₁やn̂⁺などをそのまま変数名に使えて便利.
実行速度比較
python sbm_python.py 8.74s user 0.09s system 354% cpu 2.492 total julia sbm_julia.jl たぶん60000sぐらい(終わらない...)
(なにか間違っているかもしれないが,) なんとjuliaのほうが圧倒的に遅くなってしまった. というか同じ量の計算をさせると終わらない... 調べてみるとeinsumがだめっぽいので,以下ではforで書き直す. (とはいえさすがに遅すぎるので何かやらかしている気がする.)
einsumをfor文で書き直す
juliaのマクロ(@のやつ)はコンパイル時に別の式に展開されるらしい. einsumのマクロもそれぞれの@einsumに対して多重のfor文を展開しているらしく,しかも単独でもnumpyのeinsumより遅いこともあるらしい.
ということで,普通にfor文による実装に変更して,実行速度を比較し直す. コードは以下.
m̂₁ = m(𝕀z₁) - transpose(𝕀z₁[i,:]) n⁺ = zeros(K, K) n⁻ = zeros(K, K) Σ⁺x𝕀z₂ = zeros(K) Σ⁻x𝕀z₂ = zeros(K) for l in 1:K for j in 1:N₂ Σ⁺x𝕀z₂[l] += X[i,j] * 𝕀z₂[j,l] Σ⁻x𝕀z₂[l] += (1 - X[i,j]) * 𝕀z₂[j,l] for k in 1:K n⁺[k,l] += 𝕀z₁[i,k] * X[i,j] * 𝕀z₂[j,l] n⁻[k,l] += (1 - X[i,j]) * 𝕀z₁[i,k] * 𝕀z₂[j,l] end end end n̂⁺ = zeros(K,K) n̂⁻ = zeros(K,K) for k in 1:K for l in 1:K n̂⁺[k,l] += n⁺[k,l] - 𝕀z₁[i,k] * Σ⁺x𝕀z₂[l] n̂⁻[k,l] += n⁻[k,l] - 𝕀z₁[i,k] * Σ⁻x𝕀z₂[l] end end α̂₁ = α₁ + m̂₁ â = a₀ + n̂⁺ b̂ = b₀ + n̂⁻ p_z₁ = α̂₁ for k in 1:K for l in 1:K p_z₁[k] *= exp(logΓ(â[k,l] + b̂[k,l])-logΓ(â[k,l])-logΓ(b̂[k,l]) \ + logΓ(â[k,l]+Σ⁺x𝕀z₂[l])+logΓ(b̂[k,l]+Σ⁻x𝕀z₂[l])-logΓ(â[k,l]+b̂[k,l]+sum(𝕀z₂,1)[l])) end end p_z₁ /= sum(p_z₁) 𝕀z₁[i,:] = onehot(sample(1:K, Weights(p_z₁[:])), K)
for...endのせいで見難く感じるが,これは普段pythonばかり書いていてfor文に拒絶反応があるからかもしれない. 書いている時の感想としては,行列の向きとか気にしなくていいので,einsumと同じ程度には書きやすい. 実際にfor文を全部とっぱらえば数式と近くなるはず.
実行速度比較
python sbm_python.py 8.74s user 0.09s system 354% cpu 2.492 total julia sbm_julia_2.jl 3.62s user 0.46s system 114% cpu 3.559 total
無事にpythonの半分以下の時間で処理が終わるようになった. 普段python使っていると無意識的にfor文を避けていたのが, juliaなら何も気にせずに普通にfor文書きまくれば良さそう.
おわりに
DTWとSBMという2つのアルゴリズムについて,pythonとjuliaでの実装を比較した.
| 書きやすさの改善 | 実行速度の改善 | |
|---|---|---|
| DTW | インデックスが1から.数字の添字 | 25.81s → 21.97s |
| SBM (einsum) | α̂₁やn̂⁺をそのまま書ける | 激遅 (やらかしているかも) |
| SBM (for) | ↑ | 8.74s → 3.62s |
pythonをjuliaで書き直すことで
- 数式の添字をそのまま書くことができ,書きやすさと可読性が向上した.
- 素直にfor文を使えば実行速度は改善した.
- juliaのeinsumは激遅だった.(僕がやらかしてるかも)
- 型の指定をしていないからか,実行速度の改善は限定的だった.
また,やっていて気づいたこととして
- jupyter notebook上で実行しつつ書くというやり方だと,コンパイル時間が以外と鬱陶しい
- a\hat はOKだけど,\hat aはだめとか.\leはOKだけど,\leqqはだめとかunicode関連で微妙につまることがあった.
この記事ではやらなかったこととして以下がある.気が向いたらやろうと思っている.
はてなだと表示が微妙だけど,jupyter とかでは綺麗に表示されて見やすいよ!(大事なこと)
追記 (2017/12/17)
Qiitaにて,juliaのコードについてのコメントをいただきました.ありがとうございます.
- DTWについて,こちらに書かれているように(Matrixの要素の型推論とベクトルの代わりにタプルを使用)コードを変更すると,数十倍程度高速化します.
- SBMについて,グローバル変数になっているパラメータにconstを指定するだけで,実行時間が90%程度になります.
もう少し自分でも高速化のために,あれこれやってみたいと思います.
参考
- Julia Advent Calendar 2017 - Qiita
- [1111.4246] The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo
- Unicodeプログラミングのすゝめ - りんごがでている
- Unicode Input · The Julia Language
- DTW (動的時間伸縮法)の実装 - やったことの説明
- pythonでNUTSの実装 - やったことの説明
- A global averaging method for dynamic time warping, with applications to clustering
- 関係データ学習の実装 PythonでStochastic Block Modelの実装 - やったことの説明
- 関係データ学習 | 書籍情報 | 株式会社 講談社サイエンティフィク
- Julia Language Programming
- Performance · Issue #1 · ahwillia/Einsum.jl · GitHub