2017-03-26

DTW (動的時間伸縮法)の実装

概要

自分の勉強のために、Dynamic Time Warpingを実装した。正弦波データでいろいろプロットした後、気温のデータに適用した。たぶんバグってないと思う。

はじめに

時系列データの類似度(距離)を計算するとき、単純には例えば各時刻での二乗誤差の平均などを求めることを思いつくが、これは以下のようなデータに対して、直感に反する結果になる。

%matplotlib inline
import numpy as np
import pylab as plt
import seaborn as sns

T = 150
t = .4

A = np.sin(np.array(range(T))/10)
B = np.sin((np.array(range(T))/10 + t*np.pi))
C = np.zeros((T))

plt.plot(A)
plt.plot(B)
plt.plot(C)
plt.show()

f:id:ksknw:20181001220748p:plain

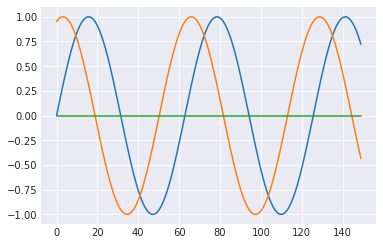
これら3つの時系列データ間の平均二乗誤差を求めると以下のようになる。

mse = lambda a,b: ((a-b)**2).mean()
print("A-B: ", mse(A,B))
print("A-C: ", mse(A,C))

A-B:  0.663947047674
A-C:  0.515002685544

この結果から、青とオレンジよりも青と緑のほうが近いということになる。これは直感に反するので、もう少し上手く距離(的なもの)を定義したい。

Dynamic Time Warping

Dynamic Time Warping (DTW)は2つの時系列データ間の距離(的なもの)を求めるアルゴリズム。
具体的には2つ時系列データの時刻をt1, t2とすると、t1,t2全ての組の誤差を計算し、それらの合計が最小になるような経路を求めるアルゴリズムになっている。
こちらのブログにアニメーションがあって良かった。

以下では、これを参考にして実装する。書いてあったアルゴリズムをできるだけそのまま書こうと思ったのでギリシャ文字とかを使っている。

δ = lambda a,b: (a - b)**2
first = lambda x: x[0]
second = lambda x: x[1]

def minVal(v1, v2, v3):
    if first(v1) <= min(first(v2), first(v3)):
        return v1, 0
    elif first(v2) <= first(v3):
        return v2, 1
    else:
        return v3, 2 

def calc_dtw(A, B):
    S = len(A)
    T = len(B)

    m = [[0 for j in range(T)] for i in range(S)]
    m[0][0] = (δ(A[0],B[0]), (-1,-1))
    for i in range(1,S):
        m[i][0] = (m[i-1][0][0] + δ(A[i], B[0]), (i-1,0))
    for j in range(1,T):
        m[0][j] = (m[0][j-1][0] + δ(A[0], B[j]), (0,j-1))

    for i in range(1,S):
        for j in range(1,T):
            minimum, index = minVal(m[i-1][j], m[i][j-1], m[i-1][j-1])
            indexes = [(i-1,j), (i,j-1), (i-1,j-1)]
            m[i][j] = (first(minimum)+δ(A[i], B[j]), indexes[index])
    return m

print("A-B: ", calc_dtw(A, B)[-1][-1][0])
print("A-C: ", calc_dtw(A, C)[-1][-1][0])

A-B:  9.67371629972
A-C:  77.2504028315

無事にA-Bのほうがだいぶ近そうという結果が得られた。

なにをやっているのかをプロットを書いて確かめる。

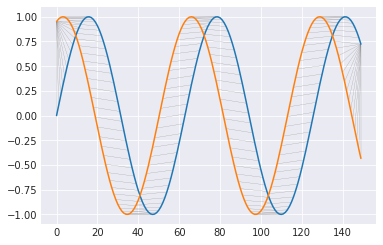
def backward(m):
    path = []
    path.append([len(m)-1, len(m[0])-1])
    while True:
        path.append(m[path[-1][0]][path[-1][1]][1])
        if path[-1]==(0,0):
            break
    path = np.array(path)
    return path

import matplotlib.gridspec as gridspec

def plot_path(path, A, B):
    gs = gridspec.GridSpec(2, 2,
                       width_ratios=[1,5],
                       height_ratios=[5,1]
                       )
    ax1 = plt.subplot(gs[0])
    ax2 = plt.subplot(gs[1])
    ax4 = plt.subplot(gs[3])
    
    list_δ = [[t[0] for t in row] for row in m]
    list_δ = np.array(list_δ)
    ax2.pcolor(list_δ, cmap=plt.cm.Blues)
    ax2.plot(path[:,1], path[:,0], c="C3")
    
    ax1.plot(A, range(len(A)))
    ax1.invert_xaxis()
    ax4.plot(B, c="C1")
    plt.show()
    
    for line in path:
        plt.plot(line, [A[line[0]], B[line[1]]], linewidth=0.2, c="gray")
    plt.plot(A)
    plt.plot(B)
    plt.show()

m = calc_dtw(A, B)
path = backward(m)
plot_path(path, A, B)

f:id:ksknw:20181001220942p:plain

f:id:ksknw:20181001221013p:plain

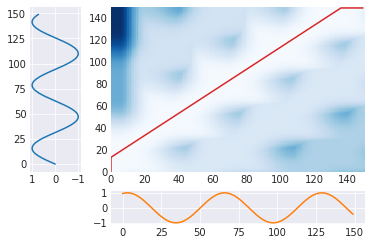
上のグラフは、t1,t2の位置での蓄積した誤差(青)と選択した経路(赤)を表している。横と下のは元の時系列データ。
また、下のグラフは選択した経路によって、2つの時系列データがどのように対応付けられたかを示している。DTWは結局、この対応する2点の(縦方向の)誤差を求めている。最初と最後は対応づけができないので、無理に合わせるしかない。

m = calc_dtw(A, C)
path = backward(m)
plot_path(path, A, C)

f:id:ksknw:20181001221044p:plain

f:id:ksknw:20181001221055p:plain

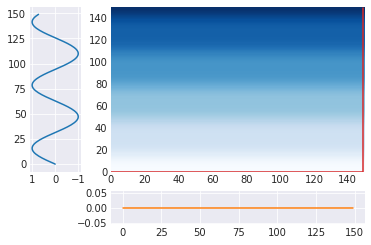
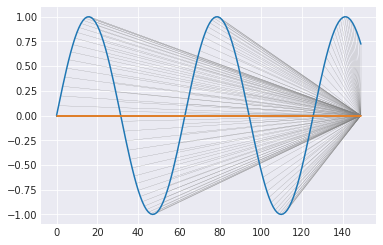
どこに対応づいていても同じだが、実装の関係からこんな感じになっていた。

長さが異なる時系列の距離(的なもの)

DTWは2つの時系列間の対応付けを重複を許す形で行うので、長さの異なる時系列データに対しても問題なく適用できる。

T = 150
S = 200
t = .4

A = np.sin(np.array(range(T))/10)
D = np.sin((np.array(range(S))/10 + t*np.pi))

m = calc_dtw(A, D)
path = backward(m)
plot_path(path, A, D)

f:id:ksknw:20181001221210p:plain

f:id:ksknw:20181001221217p:plain

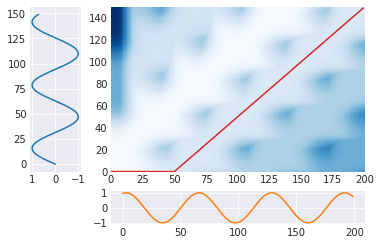
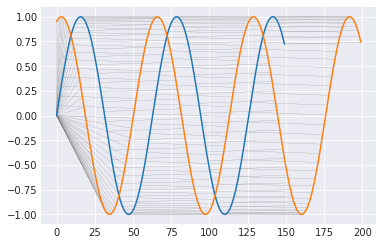
位相をだんだんずらしていったときの挙動

2つの正弦波の位相を徐々にずらしていったときに、MSEおよびDTWが距離(的なもの)をどのように評価するのかをみてみる。

list_dtw_AB = []
list_mse_AB = []
list_dtw_AC = []
list_mse_AC = []
for t in np.arange(0, 2, 0.1):
    T = 150
    A = np.sin(np.array(range(T))/10)
    B = np.sin((np.array(range(T))/10 + t*np.pi))
    list_dtw_AB.append(calc_dtw(A, B)[-1][-1][0])
    list_mse_AB.append(mse(A,B))
    list_dtw_AC.append(calc_dtw(A, C)[-1][-1][0])
    list_mse_AC.append(mse(A,C))

plt.plot(list_mse_AB, label="mse_AB")
plt.plot(list_mse_AC, label="mse_AC")
plt.legend()
plt.show()

plt.plot(list_dtw_AB, label="dtw_AB")
plt.plot(list_dtw_AC, label="dtw_AC")
plt.legend()
plt.show()

f:id:ksknw:20181001221302p:plain

f:id:ksknw:20181001221315p:plain

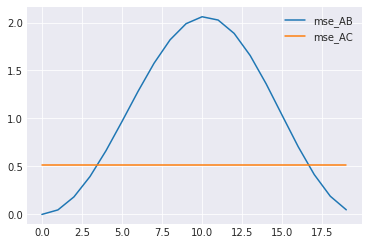
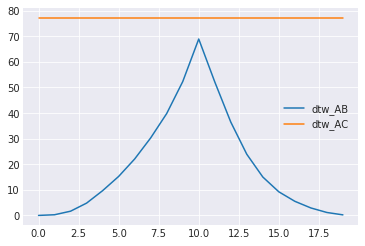
はじめの例で見たようにMSEは位相が少しずれるとy=0のほうが近いと評価してしまう。
DTWも、おそらく端の対応付けから、値は変化するが、y=0のほうが近いと評価されることはない。
(なんで尖ってるんだ...?)

実データ（国内１週間の気温データ）

正弦波ばっかりいじっててもあれなので、気象庁のサイトから適当な地点の1週間分の気温データを落として、各2点間のDTWを求める。
はじめは北海道と沖縄も入れてやったけど、その2つだけ他と離れすぎていて、グラフが見にくかったのでやめた。

また、本当は海外の「同じ時刻」のデータを持ってきて、時差があるけど云々をやりたかったが、めんどくさくなってやめた。

import pandas  as pd

data = pd.read_csv("./data2.csv", encoding='SHIFT-JIS',skiprows=[0,1, 3,4])
data.index = data["Unnamed: 0"]
data = data[data.columns[1::3]]
print(data.columns.get_values())
data.head()

['名古屋' '豊中' '八戸' '鹿児島' '福岡' '秋田' '盛岡' '山形' '仙台' '福島' 'つくば（館野）' '宇都宮' 'さいたま'
 '千葉' '東京' '新潟' '前橋' '河口湖' '甲府' '静岡' '横浜' '軽井沢' '岐阜' '富山' '金沢' '津' '大津'
 '敦賀' '京都' '奈良' '和歌山' '神戸' '岡山' '鳥取' '松江' '呉' '山口' '松山' '高知' '徳島' '高松' '大分'
 '宮崎' '熊本' '佐賀' '佐世保']

	名古屋	豊中	八戸	鹿児島	福岡	秋田	盛岡	山形	仙台	福島	...	山口	松山	高知	徳島	高松	大分	宮崎	熊本	佐賀	佐世保
Unnamed: 0
2017/3/18 1:00:00	6.4	3.8	-0.4	9.8	7.8	1.4	-0.1	2.0	3.6	4.3	...	3.4	6.1	6.6	7.2	5.4	6.2	6.8	7.8	6.4	7.5
2017/3/18 2:00:00	5.3	3.4	-0.4	9.5	7.0	0.9	0.0	2.2	3.3	4.7	...	3.0	5.6	6.0	6.4	4.7	5.9	6.8	6.1	5.9	6.8
2017/3/18 3:00:00	5.7	2.7	0.0	9.0	7.0	0.2	-0.6	2.0	3.1	5.0	...	2.3	5.4	5.4	6.5	4.0	4.9	6.0	5.8	4.9	6.2
2017/3/18 4:00:00	5.2	2.1	0.5	8.4	6.3	0.2	-1.3	1.5	3.0	5.8	...	1.9	5.3	5.2	6.0	4.1	4.2	5.6	5.3	4.9	6.1
2017/3/18 5:00:00	4.5	2.0	0.8	9.1	6.1	-0.2	-0.6	0.3	3.8	5.7	...	1.7	4.9	4.8	4.5	3.0	3.8	5.1	4.5	4.2	5.7

5 rows × 46 columns

import matplotlib.font_manager as fm
font = {'family' : 'TakaoGothic'}
plt.rc('font', **font)

data.plot(figsize=(15,6), legend=False)
plt.show()

f:id:ksknw:20170326233352p:plain

dtw = []
from itertools import product
for i,(key1, key2) in enumerate(product(data.columns, data.columns)):
    dtw.append(calc_dtw(data[key1].get_values(),
                        data[key2].get_values())[-1][-1][0])

dtw = np.array(dtw).reshape(len(data.columns), -1)

fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111)
ax.set_aspect("equal")
plt.pcolor(dtw, cmap=plt.cm.Blues)
plt.xlim(xmax=46)
plt.ylim(ymax=46)
plt.xticks(np.arange(0.5, len(data.columns)+0.5), list(data.columns), rotation=90)
plt.yticks(np.arange(0.5, len(data.columns)+0.5), list(data.columns))
plt.colorbar()
plt.show()

f:id:ksknw:20170326233404p:plain

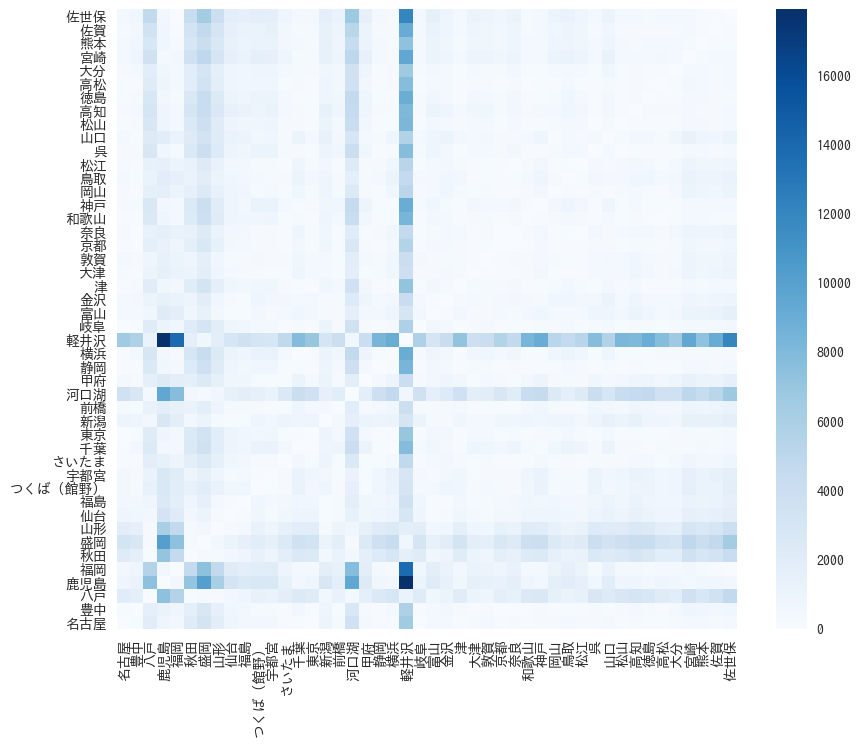
軽井沢、河口湖は他の地点と結構違う。リゾート地ということなんだろうか。

なんとなく東北と九州は気候が結構違うのかなと思った。

おまけ

こういう行列を見ると、ここから色々できそうな気がしてしまう。

tSNE

距離行列あるならtSNEできる気がするので、scikit-learnに突っ込んでみる。

from sklearn.manifold import TSNE
tsne = TSNE(metric="precomputed")

tsned = tsne.fit_transform(dtw)

plt.scatter(tsned[:,0], tsned[:,1])
for d,u in zip(tsned, data.columns):
    plt.text(d[0], d[1], u)

f:id:ksknw:20170326233419p:plain

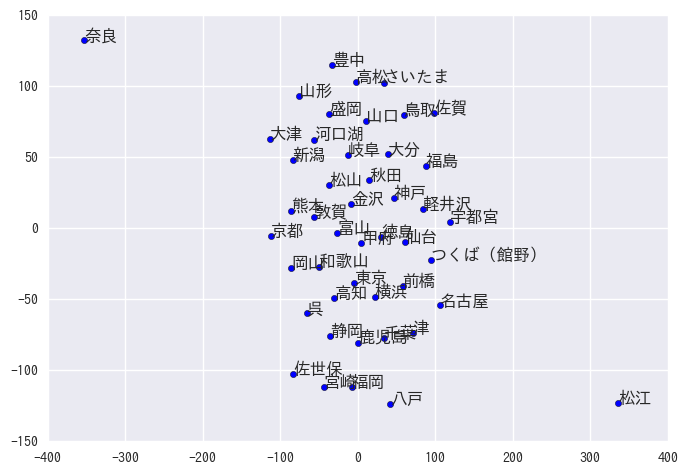
思ってたのと違う図が得られたけど、なんか間違ってる??

スペクトルクラスタリング

類似度という関係データ、しかも対称行列だということでスペクトルクラスタリングをやる。以前書いたものからコードをコピペしてくる。(みんなノートブックのコードの再利用ってどうしてんの)

import scipy.linalg
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA

def plot_matrix(matrix, clusters=None):
    f, ax = plt.subplots(figsize=(10, 10))
    plt.pcolor(matrix, cmap=plt.cm.Blues )

    if not clusters is None:
        clusters_diff = np.r_[[0], np.diff(clusters)]
        for i,c in enumerate(clusters_diff):
            if c==1:
                ax.axhline(i, c="grey") #, linewidth=1)
                ax.axvline(i, c="grey")#, linewidth=1)
    plt.show()
    
def kmeans(eigen_vector, unames, n_clusters):
    kmean = KMeans(n_clusters=n_clusters)
    clusters = kmean.fit_predict(eigen_vector)
    cluster_uname = list(zip(clusters, unames))
    cluster_uname.sort(key=lambda x:x[0])
    return clusters

D = np.eye(dtw.shape[0]) * dtw.sum(axis=0)
X = np.mat(dtw)
K = 5
hi = K-1
lo = 0

L = D - X
L_rw = np.dot(np.linalg.inv(D) , L)  # D**(-1) * L 
eigen_value, eigen_vector = scipy.linalg.eigh(L_rw,eigvals=(lo,hi))

clusters = kmeans(eigen_vector, data.columns, K)

decomp = PCA()
decomped = decomp.fit_transform(eigen_vector)

plt.figure(figsize=(7,7))
plt.scatter(decomped[:,0], decomped[:,1], c=clusters, linewidths=0, cmap=plt.cm.jet)
for d,u in zip(decomped, data.columns):
    plt.text(d[0], d[1], u)
plt.show()

f:id:ksknw:20170326233430p:plain

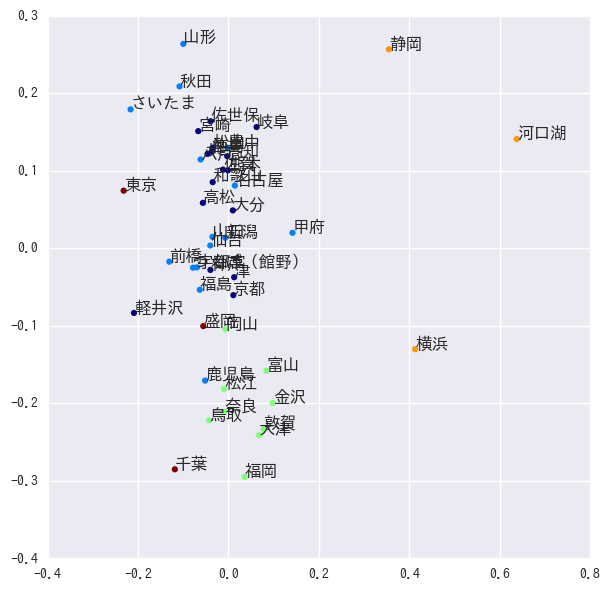
近い地域が同じクラスタになっているかと思ったら、そうでもない部分もあったり。

この１週間は似てたのかもしれないし、本当はデータを見ないとなぁと思いつつ、面倒なので終わり。

おわりに

自分の勉強のためにDTWの実装をやって、色々なデータを突っ込んでみた。今回はスペクトルクラスタリングをやったけど、参考にした論文やブログでは、重心を求めてkmeansでクラスタリングとかをやっているので、そのあたりもやってみたいなと思う。

参考

2017-03-11

numpyのarrayとmatrixの書き方の違い

はじめに
- 環境
ベクトルと行列ベクトル
トレース，行列式と逆行列
ベクトルの内積
行列とベクトルの積
行列の積
要素ごとの積 (アダマール積)
ベクトルから行列 (テンソル積 ?)
その他，関係ありそうだけど使ってない関数
おわりに

はじめに

numpyの行列関連の演算がわからなくなってググることがよくある．また，動くことは動くがもう少し綺麗にならないかと思うこともよくある．

行列を表すために，numpyではarrayとmatrixを使うことができる．
しかし，掛け算の挙動などが，これら2つで異なるためにさらにややこしい印象がある．

自分用備忘録のためにarray，matrixそれぞれで特定の演算をするためにはどうすればいいかをまとめる．

色々な関数(特にnp.tensordotとか)でこれらの演算はできるが，自分が使うだろうなと思うものだけ書く．

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

環境

import sys
version = sys.version_info
print("Python ",version.major,".",version.minor)
import numpy as np
print("numpy",np.__version__)

Python  3 . 6
numpy 1.11.3

ベクトルと行列ベクトル ${\bf x},A$

以下では，ベクトル $\bf{x}$ と行列 $A$ を使う．
${\bf x} \in \mathbb{R}^2$
$A \in \mathbb{R}^{2\times 2}$

x_a = np.array([i for i in range(1,3)])
x_m = np.mat([i for i in range(1,3)] ).T

A_a = np.array([[i*2+j for i in range(2)] for j in range(2)])
A_m = np.mat([[i*2+j for i in range(2)] for j in range(2)])

"----np.array:----"
A_a
x_a

"----np.matrix:----"
A_m
x_m

'----np.array:----'
array([[0, 2],
       [1, 3]])
array([1, 2])
'----np.matrix:----'
matrix([[0, 2],
        [1, 3]])
matrix([[1],
        [2]])

np.matrix型のベクトルは転置することで列ベクトルにできる．
np.array型もnp.transpose([x_a])と書くと列ベクトルっぽくなるが，後の処理が面倒になるのでしない．

トレース，行列式と逆行列 $\mathrm{trace(A)}, \mathrm{det}(A), A^{-1}$

ありそうだけど，matrix型にdet関数がない．(ないよね?)

"----np.array:----"
np.trace(A_a) 
np.linalg.det(A_a)
np.linalg.inv(A_a) 

"----np.matrix:----"
A_m.trace()
np.linalg.det(A_m)
A_m.I
A_m**-1

'----np.array:----'
3
-2.0
array([[-1.5,  1. ],
       [ 0.5,  0. ]])

'----np.matrix:----'
matrix([[3]])
-2.0
matrix([[-1.5,  1. ],
        [ 0.5,  0. ]])
matrix([[-1.5,  1. ],
        [ 0.5,  0. ]])

ベクトルの内積 $x・x$

array型はnp.dotもしくはx_a.dotで明示的に書かないといけない．

"----np.array:----"
np.dot(x_a, x_a) # arrayはnp.dotを使う．

"----np.matrix:----"
x_m.T * x_m # matrixは掛けるだけでいい

'----np.array:----'
5

'----np.matrix:----'
matrix([[5]])

行列とベクトルの積 $Ax$

上と同じ． matrix型は列ベクトルと行ベクトルがちゃんと結果に反映される．

"----np.array:----"
np.dot(A_a, x_a)
np.dot(x_a ,A_a)

"----np.mat:----"
A_m  * x_m
x_m.T * A_m

'----np.array:----'
array([4, 7])
array([2, 8])

'----np.mat:----'
matrix([[4],
        [7]])
matrix([[2, 8]])

行列の積 $AA, A^\top A$

転置が入ったりすると，arrayではやや面倒になる．
matrixではべき乗はこの積になる．

"----np.array:----"
np.dot(A_a, A_a)
np.dot(np.transpose(A_a), A_a) # 転置が入ると面倒

"----np.mat:----"
A_m  * A_m
A_m**2  # matrixのべき乗はこの積になる
A_m.T * A_m

'----np.array:----'
array([[ 2,  6],
       [ 3, 11]])
array([[ 1,  3],
       [ 3, 13]])

'----np.mat:----'
matrix([[ 2,  6],
        [ 3, 11]])
matrix([[ 2,  6],
        [ 3, 11]])
matrix([[ 1,  3],
        [ 3, 13]])

要素ごとの積 (アダマール積) $C_{ij} = A_{ij}B_{ij}$

array型は*が要素ごとの積になっている．
一方でmatrix型はnp.multiply関数を使う必要がある．
特にべき乗などがある場合には一旦array型に変換するほうが楽かもしれない．

"----np.array:----"
A_a * A_a
A_a ** 3 # arrayのべき乗はこの積

"----np.mat:----"
np.multiply(A_m, A_m) # matrixでは面倒
np.multiply(np.multiply(A_m, A_m), A_m)

np.mat(A_m.A**3) # .Aで一旦arrayに変換したほうが短い

'----np.array:----'
array([[0, 4],
       [1, 9]])
array([[ 0,  8],
       [ 1, 27]])

'----np.mat:----'
matrix([[0, 4],
        [1, 9]])
matrix([[ 0,  8],
        [ 1, 27]])
matrix([[ 0,  8],
        [ 1, 27]])

ベクトルから行列 (テンソル積 ?) $B_{ij} = x_ix_j, B_{ijk} = A_{ij}x_{k}$

(3次元以上の多次元配列のことをテンソルと呼ぶ文化圏にいます．)

ベクトルから行列を作ったり，行列からテンソルを作ったりする．
これはテンソル積なのか?

array型はtensordot(axes=0)を使う． matrix型はベクトル同士だとただ掛けるだけでできる．一方で，出力がテンソルになる計算はできない．

"----np.array:----"
np.tensordot(x_a, x_a, axes=0) # axesによって別の積になる
np.tensordot(x_a, A_a,  axes=0)

"----np.mat:----"
x_m * x_m.T # ベクトルはこれでいける
x_m * A_m # 答えがテンソルになる演算はできない．

'----np.array:----'
array([[1, 2],
       [2, 4]])
array([[[0, 2],
        [1, 3]],
       [[0, 4],
        [2, 6]]])

'----np.mat:----'
matrix([[1, 2],
        [2, 4]])
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-9-ede3e147096b> in <module>()
      5 "----np.mat:----"
      6 x_m * x_m.T
----> 7 x_m * A_m
/home/kei/anaconda3/envs/tensorflow/lib/python3.6/site-packages/numpy/matrixlib/defmatrix.py in __mul__(self, other)
    341         if isinstance(other, (N.ndarray, list, tuple)) :
    342             # This promotes 1-D vectors to row vectors
--> 343             return N.dot(self, asmatrix(other))
    344         if isscalar(other) or not hasattr(other, '__rmul__') :
    345             return N.dot(self, other)
ValueError: shapes (2,1) and (2,2) not aligned: 1 (dim 1) != 2 (dim 0)

その他，関係ありそうだけど使ってない関数

なんか色々あるけど，よく知らないので使ってない．

おわりに

記述が楽なので，matrixを使って書いてしまうことが多いけど，3次元以上はarrayで書くことになるので，慣れてないとバグを生む可能性が高い気がする．皆さんどうしてるんですか．

2017-03-05

関係データ学習の実装 MovieLensの行列分解

概要

関係データ学習の後半のうち，行列分解を実装した． lossが下がっているので，たぶん合っていると思うが，分解したあとのベクトルを見るとよくわからない．

はじめに

以前こんなものをやった． ksknw.hatenablog.com

前半部分は終わったので(SBMのことは置いといて)，後半部分の実装をやる．今回は行列分解を実装する．

www.kspub.co.jp

MovieLensデータ

MovieLens 100K Dataset | GroupLens

これといって分解したい行列データもなかったので，本に書いてあったデータを使うことにする． MovieLensにはユーザが映画を評価したデータが含まれている．
データを作成した時期によってデータのサイズが違うらしいが，今回は一番小さいサイズのデータを使う．
このデータには943人のユーザの映画の評価(1から5)が含まれている．
映画は1682本で各ユーザはこれらのうち少なくとも5本を評価している．
とりあえずデータを見てプロットする．

%matplotlib inline
import pylab as plt
import seaborn
import numpy as np
import pandas as pd
data = pd.read_csv("./ml-100k/u.data", names=["uid", "mid", "rating", "timestamp"], sep="\t")
data

	uid	mid	rating	timestamp
0	196	242	3	881250949
1	186	302	3	891717742
2	22	377	1	878887116
3	244	51	2	880606923
4	166	346	1	886397596
29	160	234	5	876861185
...	...	...	...	...
99995	880	476	3	880175444
99996	716	204	5	879795543
99997	276	1090	1	874795795
99998	13	225	2	882399156
99999	12	203	3	879959583

100000 rows × 4 columns

X = np.zeros((data["uid"].max(), data["mid"].max()))
for i,item in data.iterrows():
    X[item["uid"]-1, item["mid"]-1] = item["rating"]

f, ax = plt.subplots(figsize=(7, 7))

import numpy.ma as ma
masked = ma.masked_where((X==0),X)


cmap = plt.cm.jet
cmap.set_bad('white',1.)
plt.pcolormesh(masked, cmap=cmap)
plt.xlabel("movie id")
plt.ylabel("user id")
plt.show()

f, ax = plt.subplots(figsize=(7, 7))

plt.pcolormesh(masked[:100, :100], cmap=cmap)
plt.xlabel("movie id")
plt.ylabel("user id")
plt.show()

f:id:ksknw:20170305215433p:plain

f:id:ksknw:20170305215506p:plain

人気の映画やよく映画を見ている人などがなんとなくわかる．多くの人が好む映画，やたら低評価ばかりつけるユーザなど色々いる．なんらかソートされていることもわかる．
また大半は欠損データである．

まずは，(練習なので)欠損データは0とレーティングされているとして行列分解する．
その後，欠損値を除外したり，補完をするアルゴリズムを実装する．
また，本に載っているアルゴリズムでは収束判定をしていたが省略する．

import copy 
original_X = copy.deepcopy(X) 

# X = X+(X==0)*3
#X = X[:100, :100]
f, ax = plt.subplots(figsize=(7, 7))
plt.pcolormesh(X[:100, :100], cmap=cmap)

f:id:ksknw:20170305215522p:plain

1次交互勾配降下法

正則化つきの行列分解は特異値分解では求まらないので，勾配法を用いる必要がある．

それぞれ5つのベクトルでユーザ，映画が表現できると考えて，行列分解する．
動けばいいやの精神で書いているので，行列の計算はあれな感じだけど許してほしい．というかnumpy.matとarray関連の正しい使い方がわからない．

1次交互勾配法は不安定で，learning_rateを少しあげたら発散した．

nb_epoch = 100
reg = 0.01

R = 5
learning_rate = 0.001

I = X.shape[0]
J = X.shape[1]
U = np.mat(np.random.random((I, R)))
V = np.mat(np.random.random((J, R)))

dU = lambda U,V: -X*V + U * (V.T*V + reg*np.mat(np.identity(R)))
dV = lambda U,V: -X.T*U + V * (U.T*U + reg*np.mat(np.identity(R)))
error = lambda U,V: 0.5*np.sum(np.array(X-U*V.T)**2) + 0.5*reg*np.sum( np.sum(np.array(U)**2,axis=0) + np.sum(np.array(V)**2,axis=0))
err_hist = []

for i in range(nb_epoch):
    e = error(U,V)
    U -= learning_rate * dU(U,V)
    V -= learning_rate * dV(U,V)
    err_hist.append(e)

def hist_plot(err_hist):
    plt.plot(err_hist)
    plt.text(len(err_hist) -5, err_hist[-1]+500 ,"%.1f"%err_hist[-1])
hist_plot(err_hist)

f:id:ksknw:20170305215543p:plain

predict = np.array(U*V.T)
np.max(predict), np.min(predict)

(10.693971705841749, -2.4352853936451466)

def compare_plot(X, predict, cmap=plt.cm.Blues, vmin=None, vmax=None):
    f, ax = plt.subplots(figsize=(14, 7))
    plt.subplot(121)
    plt.pcolormesh(X[:100, :100], cmap=cmap, vmin=vmin, vmax=vmax)
    plt.xlabel("movie id")
    plt.ylabel("user id")
    
    plt.subplot(122)
    plt.pcolormesh(predict[:100, :100], cmap=cmap, vmin=vmin, vmax=vmax)
    plt.xlabel("movie id")
    plt.ylabel("user id")

    plt.show()
compare_plot(X, predict)

f:id:ksknw:20170305215555p:plain

最大値，最小値がずれているのでJetだと見にくかったので，青だけでプロットしている．
なんとなく出来ている気がする．

擬似2次交互勾配法

1次勾配だけだと収束が不安定で学習率をあまり大きくすることができず，収束が遅い．
2次勾配を使うことで収束を早くすることができる．

learning_rate = 1.

I = X.shape[0]
J = X.shape[1]
U = np.mat(np.random.random((I, R)))
V = np.mat(np.random.random((J, R)))
err_hist2 = []

for i in range(nb_epoch):
    e = error(U,V)
    U = (1-learning_rate)*U + learning_rate * X*V*((V.T*V+reg*np.mat(np.identity(R))).I)
    V = (1-learning_rate)*V + learning_rate * X.T*U*((U.T*U+reg*np.mat(np.identity(R))).I)
    err_hist2.append(e)

hist_plot(err_hist)
hist_plot(err_hist2)

f:id:ksknw:20170305215610p:plain

predict = np.array(U*V.T)
np.max(predict), np.min(predict)

(10.414641991236321, -2.2410733139172789)

compare_plot(X, predict)

f:id:ksknw:20170305215631p:plain

学習率を1にしても発散せず，1次勾配(青)よりも2次勾配(緑)を利用したものは早く収束するようになった．

制約付きの最適化

ここまでの実装では，推定した評価値が負の値になっている． U，Vに制約をつけることで0以上の値にすることができる． (評価値は1から5までなので本当はもう少し制約しないといけないがどうするのかはわからない．)

具体的には，負の値をとった要素を0に射影しながら最適化する．

learning_rate = 1.

I = X.shape[0]
J = X.shape[1]
U = np.mat(np.random.random((I, R)))
V = np.mat(np.random.random((J, R)))
err_hist_con = []

for i in range(nb_epoch):
    e = error(U,V)
    U = (1-learning_rate)*U + learning_rate * X*V*((V.T*V+reg*np.mat(np.identity(R))).I)
    U = np.maximum(U, 0, U)
    V = (1-learning_rate)*V + learning_rate * X.T*U*((U.T*U+reg*np.mat(np.identity(R))).I)
    V = np.maximum(V, 0, V)

    err_hist_con.append(e)

hist_plot(err_hist_con)

f:id:ksknw:20170305215653p:plain

predict = np.array(U*V.T)
np.max(predict), np.min(predict)

(8.9972633401464464, 0.0)

ちゃんと0以上に制約されている．

compare_plot(X, predict)

f:id:ksknw:20170305215708p:plain

欠損値をちゃんとやる

ここまでは欠損値を全て0だと仮定して実装した．

以下では欠損値を除外して行列分解する方法と補完する方法を行う．

除外する方法

lossの計算およびU，Vの勾配の計算のときに，欠損した値は利用しない．
実装が楽なので1次勾配を利用する方法で実装した．

M = np.array((X!=0)*1)

I = X.shape[0]
J = X.shape[1]
U = np.mat(np.abs(np.random.random((I, R))))
V = np.mat(np.abs(np.random.random((J, R))))

dU = lambda U,V: -(np.array(X - U*V.T)*M)*V   + reg*U
dV = lambda U,V: -(np.array(X - U*V.T)*M).T*U + reg*V
error = lambda U,V: 0.5*np.sum((np.array(X-U*V.T)*M)**2) + 0.5*reg*np.sum( np.sum(np.array(U)**2,axis=0) + np.sum(np.array(V)**2,axis=0))
err_hist = []

for i in range(nb_epoch):
    e = error(U,V)
    U = (1-learning_rate)*U + learning_rate * X*V*((V.T*V+reg*np.mat(np.identity(R))).I)
    V = (1-learning_rate)*V + learning_rate * X.T*U*((U.T*U+reg*np.mat(np.identity(R))).I)
    err_hist.append(e)
hist_plot(err_hist)

f:id:ksknw:20170305215722p:plain

predict = np.array(U*V.T)
np.max(predict), np.min(predict)

(10.414841938424392, -2.2413625198086238)

import numpy.ma as ma
masked_predict = ma.masked_where((X==0),predict)

compare_plot(masked[:100, :100], masked_predict, cmap=cmap, vmin=1, vmax=5)
compare_plot(masked[:100, :100], predict, cmap=cmap, vmin=1, vmax=5)

f:id:ksknw:20170305215738p:plain

f:id:ksknw:20170305215755p:plain

全体的に評価が低めな感じになってしまっている．また，欠損していた部分も低めの値で埋まっている感じ．

補完する方法

こちらの方法では欠損値を毎回，予測値で補完する．欠損値を除外する方法と等価らしいので，こちらは2次勾配を使って，制約もつける方法で実装する．

M_hat = np.array((X==0)*1)

I = X.shape[0]
J = X.shape[1]
U = np.mat(np.abs(np.random.random((I, R))))
V = np.mat(np.abs(np.random.random((J, R))))
error = lambda U,V: 0.5*np.sum((np.array(X-U*V.T)*M)**2) + 0.5*reg*np.sum( np.sum(np.array(U)**2,axis=0) + np.sum(np.array(V)**2,axis=0))

err_hist_comp = []

X_hat = X + np.mat(np.array(U*V.T)*M_hat)

for i in range(nb_epoch):
    e = error(U,V)
    U = (1-learning_rate)*U + learning_rate * X_hat*V*((V.T*V+reg*np.mat(np.identity(R))).I)
    U = np.maximum(U, 0, U)
    X_hat = X + np.mat(np.array(U*V.T)*M_hat)
    V = (1-learning_rate)*V + learning_rate * X_hat.T*U*((U.T*U+reg*np.mat(np.identity(R))).I)
    V = np.maximum(V, 0, V)
    X_hat = X + np.mat(np.array(U*V.T)*M_hat)
    err_hist_comp.append(e)
hist_plot(err_hist_comp)

f:id:ksknw:20170305215813p:plain

predict = np.array(U*V.T)
np.max(predict), np.min(predict)

(7.7494405681324903, 0.0082254500224862269)

import numpy.ma as ma
masked_predict = ma.masked_where((X==0),predict)

compare_plot(masked[:100, :100], masked_predict, cmap=cmap, vmin=1, vmax=5)
compare_plot(masked[:100, :100], predict, cmap=cmap, vmin=1, vmax=5)

f:id:ksknw:20170305215827p:plain

f:id:ksknw:20170305215841p:plain

だいたいできているような気がする．

ベクトルをみる

行列分解で得られたU，Vでは近いユーザもしくは映画が近いベクトルで表現される．
MovieLensには評価だけでなく，どんな映画かやどんなユーザかといった情報も含まれている．
これらとU,Vを比較することで，正しい行列分解ができたかを評価する．

普段あまり映画を見ないのと，古い映画のデータしかないので，Toy StoryとGolden Eyeぐらいしかわからなかった．
ユーザの属性ならなんとなくわかるので，そちらを使う．ユーザの情報は以下．

user_info = pd.read_csv('ml-100k/u.user', sep='|',
                         encoding='latin-1',header=None)
user_info

	0	1	2	3	4
0	1	24	M	technician	85711
1	2	53	F	other	94043
2	3	23	M	writer	32067
3	4	24	M	technician	43537
...	...	...	...	...	...
937	938	38	F	technician	55038
938	939	26	F	student	33319
939	940	32	M	administrator	02215
940	941	20	M	student	97229
941	942	48	F	librarian	78209
942	943	22	M	student	77841

943 rows × 5 columns

職業がわかりやすそうなので，プロットしてみる．

from sklearn.manifold import TSNE
tsne = TSNE()
tsned = tsne.fit_transform(U) 
plt.scatter(tsned[:,0], tsned[:,1], c=(user_info[3]=="scientist"), cmap=plt.cm.Accent, marker=".")
plt.show()
plt.scatter(tsned[:,0], tsned[:,1], c=(user_info[3]=="engineer"), cmap=plt.cm.Accent, marker=".")
plt.show()
plt.scatter(tsned[:,0], tsned[:,1], c=(user_info[3]=="student"), cmap=plt.cm.Accent, marker=".")
plt.show()

f:id:ksknw:20170305215854p:plain

f:id:ksknw:20170305215903p:plain

f:id:ksknw:20170305215911p:plain

そうでもない感じだったので，うまくいっているのかよくわからない．

まとめ

勉強のために行列分解の実装をした．収束はしたけど，うまくいっているのかはよくわからない．

参考

2017-01-08

EmacsでPythonとTeXとMarkdownを書いてる動画と使ってるパッケージ

はじめに

今年は頑張ってアウトプットを増やすことを目標にした。とはいえ、特に書くこともなかったので、Emacsについて書く。

正月やることがなかったので、またEmacsの設定を見なおした。 Emacs Rocksという動画に触発されて、動画で説明することにした。普段pythonとTeXとMarkdownしか書かないので、それらについての設定しかできていない。

環境

Emacs 24.5
Ubuntu 14.04
.emacs

github.com

python

youtu.be

python modeはこのころとあまり変わっていない。

yasnippet
予め登録されているnpとかmainとかの後にtabを打つと、スニペットを挿入してくれる。自分でスニペットを登録できるので、独自のライブラリに関するスニペットとかも作れて便利。
jedi
jediはオムニ補完、つまり文法的な部分をある程度汲んだ上で補完をしてくれる。動画ではやらなかったが関数定義にジャンプしたりもできる。 importした直後とかはたまに補完候補をだすのに数秒かかることもある。
flymake-python-pyflakes
文法エラーやwarningの表示。 flymake-cursorを入れないとカーソル位置のエラーが表示されなかったようなそうでもなかったような気がする。
py-autopep8
pep8準拠のコードに自動的に修正。演算子の両側にスペースを入れたり、改行を入れたり。 after-save-hookに登録して、保存時に修正するといい感じ。
iedit
複数箇所の同時編集。変数名を変えたいときに便利。範囲を関数内に限定したり、手動で範囲を決めたりできる。 multiple-cursorsとどっちがいいんでしょうか。
smartparens
括弧などの補完。補完もそうだけど、範囲選択して括弧を入力すると、その範囲を括弧で囲ってくれるのがいい。
highlight-parentheses
括弧の色を深さで変える。趣味。

TeX

youtu.be

AUCTeX
以前までYaTeXを使っていたけど、どちらがいいかわからなかったので、とりあえず使ってみている。数式に関するショートカットがなくなったけど、yasnippet使うしどっちでもいい気がする。 C-c C-c でlatexmkを呼ぶようにできるらしいので、その点はこっちのほうがいいかも。
yasnippet
機能はpythonと同じだが、複雑な構文が多いのでかなり役に立つ。 figureの構文とか覚えてられないし。 TeX固有の機能として、cite + Tabとかref+Tabでreftexを呼ぶようになっている。デフォルトのままなので、自分の環境に合わせてもうちょっといじったほうがいいかなと思っている。
reftex
bibファイルは使い回しなので、どういう名前で登録したか覚えていないし、長い文章を書いていると、\labelで設定した名前なんか忘れる。 reftexは参考文献入れるときや\refを使うときに、名前を補完してくれる。参考文献は特に著者名前でもキーワードでもヒットするので便利。
同じbibファイルを使いまわすときは、default-bibliographyに登録しておくと便利。
magic latex buffer
\beginとか\endを▽△に変えたり、数式を表示したり、見やすいように色々やってくれる。コマンドのタイポに気づきやすい。数式以外の場所で"_"を打っても添字扱いされるところが少し困る。

Markdown

youtu.be

OrgTbl
markdownで表を書いてると、自分で合わせない限り縦棒がずれているので見にくい。 orgの表を書くモードをMarkdownモードでも使えるので、それを使う。 orgとMarkdownで一部書式が違うので、保存時に変換している。
flymd
Markdownのリアルタイムプレビューはいくつかパッケージがあるけど、今はflymdを使っている。画像や数式もちゃんと表示されるのでいい。
misc
研究ノート的なものをmarkdownで書いているので、C-x C-nで常に同じファイルが開くようになっている。 org-modeでいいじゃないかという気もしている。

その他

git-gutter-fringeの見た目をちょっといじって使っている。いい感じ。

f:id:ksknw:20170108204246p:plain

今後の課題

未だに改行をEnterでしか打てないので、C-mとかC-jとか使っていきたい。

参考

2016-12-29

関係データ学習の実装ツイッターデータのスペクトルクラスタリングとSBM

概要

関係データ学習の学習のために，自分で実装して理解する．ツイッターのフォローフォロワー関係を使って，グラフラプラシアンを求めスペクトルクラスタリングを行った．その結果，なんとなくクラスタリングできた．また，確率的ブロックモデルによる非対称データクラスタリングをStanによって実装しようとした．これはうまくいっていない．

はじめに

関係データ学習という本を買って読んでいる．

www.kspub.co.jp

本の内容は前半と後半に分かれていて，前半は関係データをスペクトルクラスタリングしたり，確率的ブロックモデルでクラスタリングしたりする話．後半は行列分解やテンソル分解の話になっている．まだ前半の途中までしか読めていないが，予想していたよりも数式が簡単だったこともあり，実際のデータに適用してみたくなった．数年前に書いたツイッターのフォローフォロワー関係をダウンロードするスクリプトを見つけたので，これを使ってデータを作り，自分のフォロー中の人たちをクラスタリングしてみることにした． (カット最小化とスペクトルクラスタリングの関係とか，まだよく理解できてないので，理論的な説明はしない．)

ツイッターデータのダウンロード

tweepyを使って関係データをダウンロードする．スクリプトは何年も前に書いたものであり，なんとなく恥ずかしいのでここでは省略するが，

自分がフォローしている人のフォローしている人を全てダウンロード．
ダウンロードした中から自分がフォローしている人たちの関係を抜き出す．

ようになっている．ツイッターのapi制限があるので，100人ちょっとだけど，それなりに時間がかかる．

ダウンロードしたのは以下のようなデータ。つながっている部分が青、ない部分が白。鍵垢のデータはとれてない部分もある。ツイッターではフォローしているがされていないなどの関係もあるので，非対称データになる．

import pandas as pd

data = pd.read_csv("./combinationTable.csv")
uname = data[:1].get_values()[0]

%matplotlib inline
import pylab as plt
import seaborn
import numpy as np

X = (data.get_values()[1:]=="True")

def plot_matrix(matrix, clusters=None):
    f, ax = plt.subplots(figsize=(10, 10))
    plt.pcolor(matrix, cmap=plt.cm.Blues )

    if not clusters is None:
        clusters_diff = np.r_[[0], np.diff(clusters)]
        print clusters_diff
        for i,c in enumerate(clusters_diff):
            if c==1:
                ax.axhline(i, c="grey") #, linewidth=1)
                ax.axvline(i, c="grey")#, linewidth=1)
    plt.savefig("../../temp.svg")
    plt.show()

plot_matrix(X)

f:id:ksknw:20161225112150p:plain

すでにある程度のクラスタができているように見える．これは自分が今まで所属した(ツイッター的意味での)クラスタを表している．自分がフォローした順にアカウントが並んでいるので，右上からだいたいポケモン，大学，大学研究室，研究者みたいな感じ．研究者クラスタ以外は知り合いをフォローしていることが多いので，数が少ない．

はじめはこの関係データを対称データに変換し，2章を参考にしつつスペクトルクラスタリングを行う．以下のように対称データに変換した．

symmetry_X = (X.T + X)
plot_matrix(symmetry_X)

f:id:ksknw:20161225112224p:plain

非正規化グラフラプラシアンに基づくスペクトルクラスタリング

対称データ $X$ とクラスタ数 $K$ が与えられたとき、非正規化グラフラプラシアン $L$ は以下のように定義される。

$L=D-X$

ここで $D$ は次数行列で、オブジェクトから伸びるリンクの総数。 $L$ をプロットすると以下。

D = np.eye(symmetry_X.shape[0]) * symmetry_X.sum(axis=0)
K = 10
L = D - X
plot_matrix(L)

f:id:ksknw:20161225125154p:plain

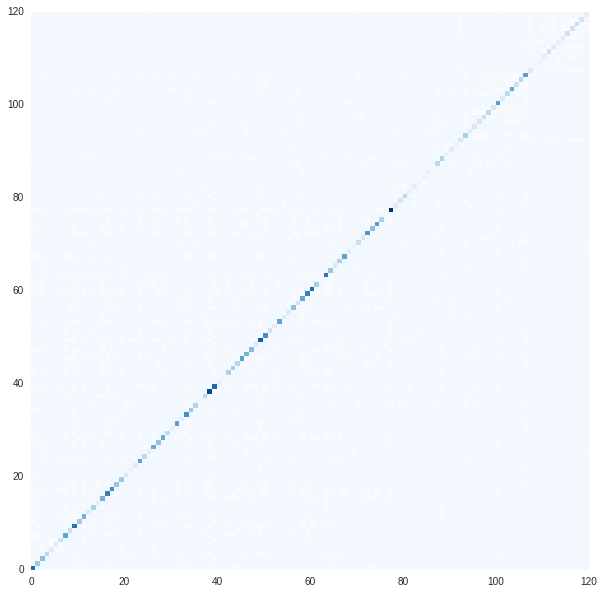
先ほどまでとはグラフの色が異なるので注意．対角成分だけ1以上の値をとるのでこんな感じの図になる。

スペクトルクラスタリングでは、以下の手順でクラスタを抽出する。

グラフラプラシアンを固有値分解して固有ベクトルを求める。
固有ベクトルをK-meansなどでクラスタリングする。

クラスタ数は適当に10とした。本来なら色々チューニングしないといけないが、面倒なので固定する。

import scipy.linalg

hi = K-1
lo = 0
eigen_value,eigen_vector = scipy.linalg.eigh(L,eigvals=(lo,hi))

def plot_eigen_vec(eigen_vector):
    plt.figure(figsize=(30,10))
    plt.plot(np.abs(eigen_vector))
    plt.show()

from sklearn.cluster import KMeans
def kmeans(eigen_vector, unames, n_clusters):
    kmean = KMeans(n_clusters=n_clusters)
    clusters = kmean.fit_predict(eigen_vector)
    cluster_uname = zip(clusters, uname)
    cluster_uname.sort(key=lambda x:x[0])
    print cluster_uname
    return clusters

def sort_by_cluster(matrix, clusters):
    sorted_mat = zip(clusters, matrix)
    sorted_mat.sort(key=lambda x:x[0])
    _,sorted_mat = zip(*sorted_mat)
    
    sorted_mat = zip(clusters, np.array(sorted_mat).T)
    sorted_mat.sort(key=lambda x:x[0])
    sorted_clusters,sorted_mat = zip(*sorted_mat)
    return np.array(sorted_mat).T, sorted_clusters

plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))
sorted_mat, sorted_clusters = sort_by_cluster(symmetry_X, clusters)

クラスタリング結果は以下。クラスタの番号順に並び替えて、境界に線を引いた。

f:id:ksknw:20161225125552p:plain

でかいクラスタが1つと1アカウントしかないクラスタがいくつかできた。正規化しない単純なグラフラプラシアンだとこういう結果になるらしい。

対称正規化グラフラプラシアンに基づくスペクトルクラスタリング

もう少し望ましいクラスタリングを得るために、グラフラプラシアンの正規化を行う。これは(緩和した)グラフカットの正規化と等価になる(?)らしいが、細かい説明は本(とその参考文献)に譲る。読まねば。

対象正規化グラフラプラシアン $L_\mathrm{sym}$ は、上で定義したグラフラプラシアン $L$ から以下のように求まる。

$L_\mathrm{sym} =D^{-\frac{1}{2}} L D^{-\frac{1}{2}}$

L = D - X
L_sym = np.dot(np.dot(scipy.linalg.sqrtm(np.linalg.inv(D)) , L) , scipy.linalg.sqrtm(np.linalg.inv(D))) # D**(-0.5) * L * D**(-0.5)
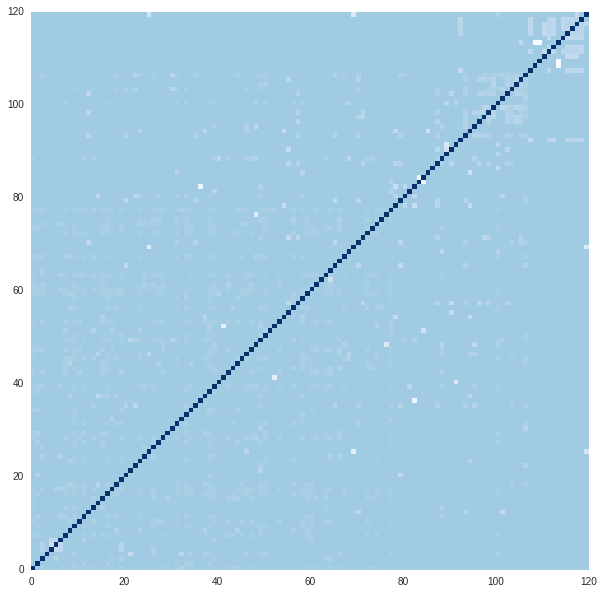
plot_matrix(L_sym)
eigen_value,eigen_vector = scipy.linalg.eigh(L_sym,eigvals=(lo,hi))
eigen_vector = eigen_vector/np.linalg.norm(eigen_vector)

対象正規化グラフラプラシアンのプロットは以下。非正規化グラフラプラシアンに比べて対角項が小さくなっている。また、クラスタリングする前に固有ベクトルを正規化している。

f:id:ksknw:20161225144212p:plain

plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))

クラスタリング結果は以下。先程に比べればだいぶ良さそうだが、真ん中の巨大なクラスタにほとんど周りとつながっていないものがいくつか含まれている。

f:id:ksknw:20161225144619p:plain

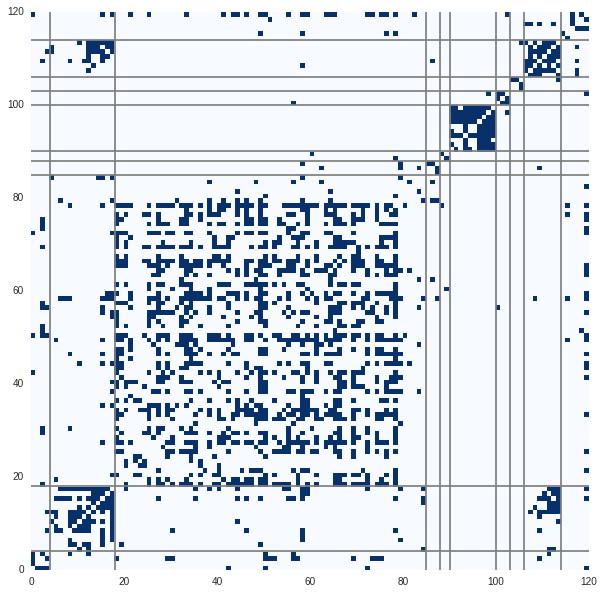
酔歩正規化グラフラプラシアン

別の正規化から導かれるグラフラプラシアンを使ってクラスタリングをする。

$L_\mathrm{rw} =D^{-1} L$

L = D - X
L_rw = np.dot(np.linalg.inv(D) , L)  # D**(-1) * L 

plot_matrix(L_rw)
eigen_value,eigen_vector = scipy.linalg.eigh(L_rw,eigvals=(lo,hi))

plot_eigen_vec(eigen_vector)
clusters = kmeans(eigen_vector, uname, K)
plot_matrix(*sort_by_cluster(symmetry_X, clusters))

f:id:ksknw:20161225145741p:plain

でかいクラスタが少し分割されて、まあこっちのほうがいいかなぁという感じ。

固有ベクトルをPCAで2次元に落としてプロットする。左でポケモンクラスタが孤立している。右に研究室のクラスタがきた。ドクターの人と先生のアカウントは研究者のクラスタとエッジをたくさんもっている。研究室が同じかつ大学の同級生は大学同級生クラスタと研究室クラスタの間に配置された。このような感じで、まあまあ妥当なクラスタリングができた。

from sklearn.decomposition import PCA
# from sklearn.manifold import TSNE
# decomp = TSNE()
decomp = PCA()
decomped = decomp.fit_transform(eigen_vector)

%matplotlib inline
plt.figure(figsize=(20,20))
for i,row in enumerate(X):
    for j,is_connected in enumerate(row):
        if is_connected:
            plt.plot(decomped[[i,j], 0], decomped[[i,j], 1], alpha=0.2,linewidth=0.3, c="gray")
plt.scatter(decomped[:,0], decomped[:,1], c=clusters, linewidths=0, cmap=plt.cm.jet)
#for d,u in zip(decomped, uname):
#    plt.text(d[0], d[1], u)
plt.show()

f:id:ksknw:20161229121731p:plain

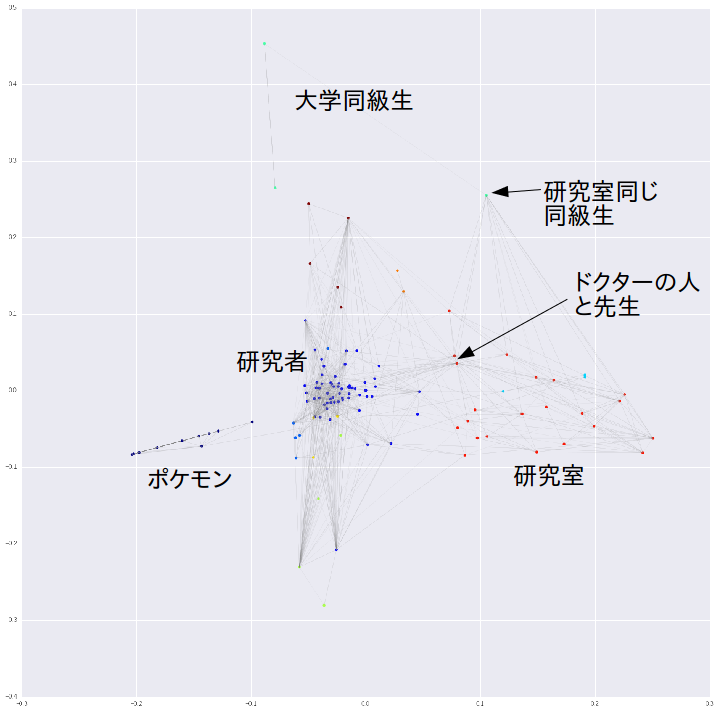
確率的ブロックモデルによる非対称データクラスタリング

ここまでは、本来非対称データであるツイッターの関係データを対称データとしてクラスタリングした。ここからは、確率的ブロックモデル(SBM)を使って非対称データのままクラスタリングする。

$i$ 番目のアカウントが $j$ 番目のアカウントをフォローしているかどうかを ${ \displaystyle x_{i,j} }$ と書く。また、 $z_{1,i}$ を $i$ 番目のアカウントが所属するフォローする側のクラスタ、 $z_{2,i}$ をフォローされる側のクラスタとする。フォローする側のクラスタとか意味がわからないかもしれないが、例えば機械学習関連のアカウントをフォローしまくっているクラスタとかそういう感じだと思う。

このときSBMでは以下の生成モデルを仮定する。

$\pi_1 \mid \alpha_1 \sim \mathrm{Dirichlet}(\alpha_1)$
$\pi_2 \mid \alpha_2 \sim \mathrm{Dirichlet}(\alpha_2)$
$z_{1,i} = k\mid \pi_1 \sim \mathrm{Discrete}(\pi_1)$
$z_{2,i} = l\mid \pi_2 \sim \mathrm{Discrete}(\pi_2)$
$\theta_{k,l} \mid a_0,b_0 \sim \mathrm{Beta}(a_0,b_0)$
${ \displaystyle x_{i,j} \mid {\theta_{k,l}} , z_{1,i}, z_{2,j} \sim \mathrm{Bernoulli}(\theta_{z_{1,i}, z_{2,j}}) }$

SBMを使うと、「フォローする(1)」と「フォローされる(2)」にわけてクラスタを考えることになる。例えば「フォロワーするクラスタ」は有名な研究者をフォローするクラスタだが、「フォローされるクラスタ」は研究室の人とかそういうことになる。うっ

SBMでは、クラスタ間の関係の強さ $\theta_{k,l}$ とそれぞれのアカウントがどのクラスタに所属するか $z_{1,i}$ 、 $z_{2,i}$ を同時に推定する。本では周辺化ギブスサンプラーによる推論方法の導出を行っている。ここでは、Stanを用いて、SBMを解くことを試みる。まずは、上の数式をそのままStanに変換すると以下のようになる。

data{
  int N;
  int K;
  int x[N, N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  int z1[N];
  int z2[N];
  vector[K] pi1;
  vector[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  matrix[K,K] theta;
}

model{
  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);

  for (i in 1:N){
    z1[i] ~ categorical(pi1);
    z2[i] ~ categorical(pi2);
  }

  for (k in 1:K){
    for(l in 1:K){
      theta[k,l] ~ beta(a0, b0);
    }
  }

  for (i in 1:N){
    for (j in 1:N){
      x[i,j] ~ bernoulli(theta[z1[i], z2[j]]);
    }
  }
}

これには色々問題があるが、特にint型の変数がparametersの中に含まれていることが問題である。 Stanでは離散的なパラメータを扱うことができないので、zで周辺化する必要がある。 zで周辺化したり、遅すぎないようにベクトルにしたりで以下のようになる。~~(たぶんあっていると思う。)~~間違っている。

data{
  int N;
  int K;
  int x[N*N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  simplex[K] pi1;
  simplex[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  vector<lower=0,upper=1>[K*K] theta;
}

model{
  real gamma[K*K];

  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);
  theta ~ beta(a0, b0);

  for (k in 1:K){
    for (l in 1:K){
      gamma[k+ K*(l-1)] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x | theta[k+ K*(l-1)]);
    }
  }
  target += log_sum_exp(gamma);
}

サンプリングする。

import pystan
data_dict= {"N":len(X),
            "K":10,
            "x":X.astype(int).reshape(-1)}
fit = pystan.stan("sbm_vector.stan", data=data_dict)
fit

            mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
alpha1[0]  2.6e7   3.1e7  5.3e7 3429.6 4934.1  3.9e4  1.2e7  1.8e8    3.0    3.2
alpha1[1]  3.2e8   3.5e8  5.0e8  3.0e5  1.4e6  3.7e7  5.4e8  1.4e9    2.0   6.44
alpha1[2]  1.0e7   6.9e6  9.7e6 460.13  1.1e6  6.9e6  1.5e7  3.4e7    2.0    2.7
alpha1[3]  2.9e7   3.6e7  5.0e7 9752.8  2.5e4  7.6e5  4.8e7  1.4e8    2.0   9.99
alpha1[4]  9.3e6   1.2e7  1.6e7   1.29  5.7e4  3.8e5  9.9e6  5.1e7    2.0   5.75
...
theta[97]   0.58    0.14   0.25   0.16    0.3    0.6   0.74   0.98    3.0   3.63
theta[98]   0.29    0.04   0.16   0.02   0.23   0.23   0.35   0.78   17.0   1.12
theta[99]   0.35    0.09   0.16   0.11   0.19   0.34   0.54   0.57    3.0   2.23
lp__       -4015   40.35  57.06  -4105  -4053  -4019  -3975  -3929    2.0  12.14

fit.plot()

f:id:ksknw:20161229165851p:plain

うまく収束しなかった。特に対策をしていないために、ラベルスイッチングが起こっているのが原因かなと思ったので、 $\theta$ の片側をorderに変えた。 0~1の制約も残さないといけないので、すこしごちゃごちゃした。

data{
  int N;
  int K;
  int x[N*N];
}

parameters{
  vector<lower=0>[K] alpha1;
  vector<lower=0>[K] alpha2;
  simplex[K] pi1;
  simplex[K] pi2;
  real mu;
  real<lower=0> sigma;
  ordered[K] theta_l[K];
}

transformed parameters{
  vector<lower=0, upper=1>[K] theta[K];
  for (k in 1:K){
    for (l in 1:K){
      theta[k][l] = inv_logit(theta_l[k][l]);
    }
  }
}

model{
  real gamma[K*K];
  pi1 ~ dirichlet(alpha1);
  pi2 ~ dirichlet(alpha2);
  for (k in 1:K)
    theta_l[k] ~ normal(mu, sigma);

  for (k in 1:K){
    for (l in 1:K){
      gamma[k+ K*(l-1)] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x | theta[k][l]);
    }
  }
  target += log_sum_exp(gamma);
}

サンプリングする。

fit2 = pystan.stan("sbm2.stan", data=data_dict)
fit2

                   mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
    alpha1[0]     2.3e7   1.3e7  2.3e7 6866.1  1.7e6  1.7e7  3.5e7  7.8e7    3.0   2.35
    alpha1[1]     4.4e7   2.0e7  3.4e7  2.1e4  7.3e6  4.3e7  6.1e7  1.1e8    3.0    2.5
    alpha1[2]     3.8e8   5.0e8  7.0e8  2.4e5  1.4e6  4.0e6  4.0e8  2.2e9    2.0   2.96
    alpha1[3]     3.6e7   3.6e7  5.1e7  5.1e6  7.1e6  9.3e6  3.9e7  1.7e8    2.0   3.64
    alpha1[4]     6.1e7   6.1e7  1.1e8  5.6e5  1.1e6  8.5e6  5.7e7  3.5e8    3.0   4.63
    alpha1[5]     3.9e7   3.6e7  5.1e7 2659.3 9569.2  8.9e6  6.2e7  1.5e8    2.0   4.23
    ...
    theta[8,9]     0.95    0.07   0.13   0.51    1.0    1.0    1.0    1.0    4.0   1.66
    theta[9,9]     0.93    0.08   0.16   0.38    1.0    1.0    1.0    1.0    4.0    1.8
    lp__          -4060    6.59  13.17  -4087  -4070  -4060  -4049  -4039    4.0   1.98

が、これもだめ。

諦めて一端ここで終わり。

追記(2017年1月5日)

上記はたぶん間違っているので、以下のようなモデルを作った。しかし、これもうまくいっていない。

data{
  int N;
  int K;
  int x[N,N];
}

parameters{
  simplex[K] pi1;
  simplex[K] pi2;
  real<lower=0> a0;
  real<lower=0> b0;
  /* vector<lower=0>[K] alpha1; */
  /* vector<lower=0>[K] alpha2; */
  matrix<lower=0, upper=1>[K,K] theta;
}

transformed parameters{
  matrix<upper=0>[K,K] soft_z[N, N];
  for (i in 1:N){
    for (j in 1:N){
      for (k in 1:K){
        for (l in 1:K){
          soft_z[i,j, k,l] = log(pi1[k]) + log(pi2[l]) + bernoulli_lpmf(x[i,j] | theta[k,l]);
        }
      }
    }
  }
}

model{
  /* pi1 ~ dirichlet(alpha1); */
  /* pi2 ~ dirichlet(alpha2); */
  to_vector(theta) ~ beta(a0, b0);

  for (i in 1:N){
    for (j in 1:N){
      target += log_sum_exp(soft_z[i,j]);
    }
  }
}

追記(2017年4月)　

続き

ksknw.hatenablog.com

おわりに

関係データ学習の学習のために，対称データのスペクトルクラスタリングと非対称データのSBMを実装した。スペクトルクラスタリングの結果、なんとなくクラスタを抽出できた。 SBMをStanで実装しようとしたが、いまいち収束しなかった。

とりあえず、最後まで読んで、頑張れたら頑張ります。

参考

関係データ学習 | 書籍情報 | 株式会社講談社サイエンティフィク

2016-12-11

Stanで気温変動のフィッティング

はじめに

この記事は Stan Advent Calendar 2016の~~n日目の記事ではありません。~~ 21日目の記事です。

話題のアヒル本~~(言われるまで何がアヒルなのかわからなかった)~~を読んだ。

statmodeling.hatenablog.com

Stanの文法を知るために買ったけれど、全体的に統計モデリング、解析について書いてあって、勉強になった。本を読んで勉強になったことはたくさんあるけど、特にグラフを死ぬほど書かないといけないという認識を持った。自分ではそれなりにグラフを書いているつもりだったけれど、pariplotとかviolinplotとかちゃんと書いたことがなかった。

せっかく本を読んだので、適当にデータをとってきて解析してAdvent Calendarなるものに挑戦しようと思っていたけど、もう埋まっていた。悲しいので一人で勝手にやることにする。よく見たら21日が空いていたので、フライングということにさせてください。

今回は特に12章を見ながら時系列データをいじくることにした。

知識がないので、間違ったことをしていたら教えていただけると嬉しいです。

データ

時系列データとして天気に関するデータを使うことにした。気象庁のサイトから天気に関するいろんなデータがダウンロードできるので利用する。

今回は愛知県の気温とか降水量とかを過去5年分ぐらいダウンロードした。日本語のファイルがやや面倒だった。

import pandas as pd
aichi = pd.read_csv("./weather_aichi.csv", encoding='SHIFT-JIS')
aichi["年"] = aichi[u"年月日"].apply(lambda x: x.split("/")[0])
aichi["月_s"] = aichi[u"年月日"].apply(lambda x: "%02d"%int(x.split("/")[1]))
aichi["日_s"] = aichi[u"年月日"].apply(lambda x: "%02d"%int(x.split("/")[2]))
aichi["m"] = aichi[u"年月日"].apply(lambda x: int(x.split("/")[1]))
aichi["d"] = aichi[u"年月日"].apply(lambda x: int(x.split("/")[2]))
aichi["is_rain"]  = aichi[u"降水量の合計(mm)"]>0
aichi = aichi.set_index(u"年月日")
month_groups = aichi.groupby("月_s")
aichi

	Unnamed: 0	平均気温(℃)	降水量の合計(mm)	年	月_s	日_s	m	d	is_rain
年月日
2011/12/3	1	12.2	8.5	2011	12	03	12	3	True
2011/12/4	2	11.9	0.0	2011	12	04	12	4	False
2011/12/5	3	10.4	0.0	2011	12	05	12	5	False
2011/12/6	4	8.0	0.5	2011	12	06	12	6	True
...	...	...	...	...	...	...	...	...	...
2016/11/30	1825	8.2	0.0	2016	11	30	11	30	False
2016/12/1	1826	12.0	0.0	2016	12	01	12	1	False
2016/12/2	1827	11.0	0.0	2016	12	02	12	2	False
2016/12/3	1828	9.8	0.0	2016	12	03	12	3	False

1828 rows × 9 columns

今回は、平均気温をモデリングしてみることにした。とりあえずグラフを書く。

%matplotlib inline 
import pylab as plt
import seaborn as sns
import matplotlib.font_manager as fm
font = {'family' : 'TakaoGothic'}
plt.rc('font', **font)

ax = aichi[[ u"平均気温(℃)"]].plot(figsize=(20,10))

f:id:ksknw:20161211134350p:plain

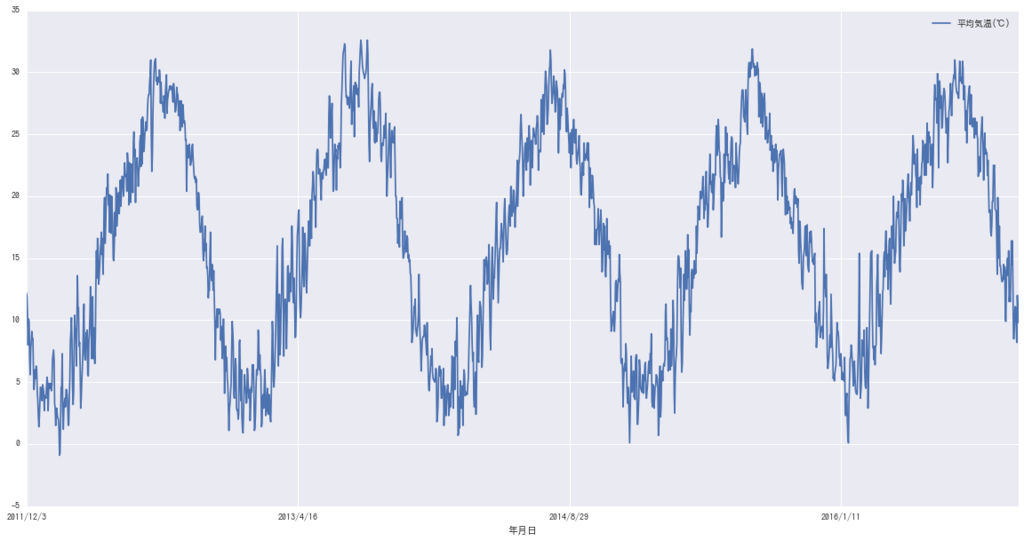
当たり前だけど春夏秋冬がある。雨のデータも後で使うのでプロットする。

ax = aichi[ u"平均気温(℃)"]["2011/12/3": "2012/12/3"].plot(figsize=(20,10))
aichi[ u"降水量の合計(mm)"]["2011/12/3": "2012/12/3"].plot( kind="bar", ax=ax)
plt.show()

f:id:ksknw:20161211134429p:plain

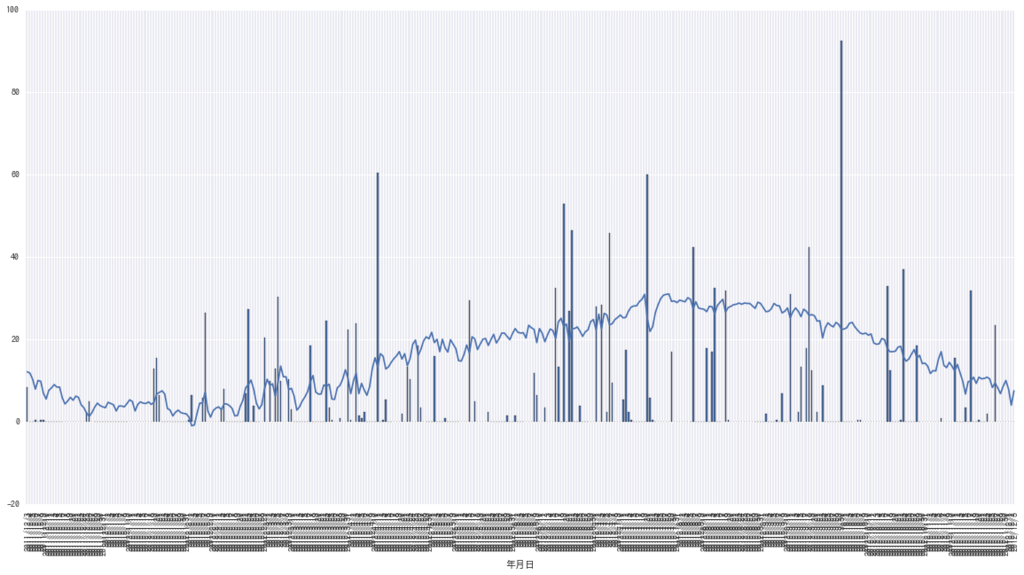
その他色々プロットを書く。

sns.pairplot(aichi[[u"平均気温(℃)",   u"降水量の合計(mm)", "m"]], hue="m", size=4)

f:id:ksknw:20161211134443p:plain

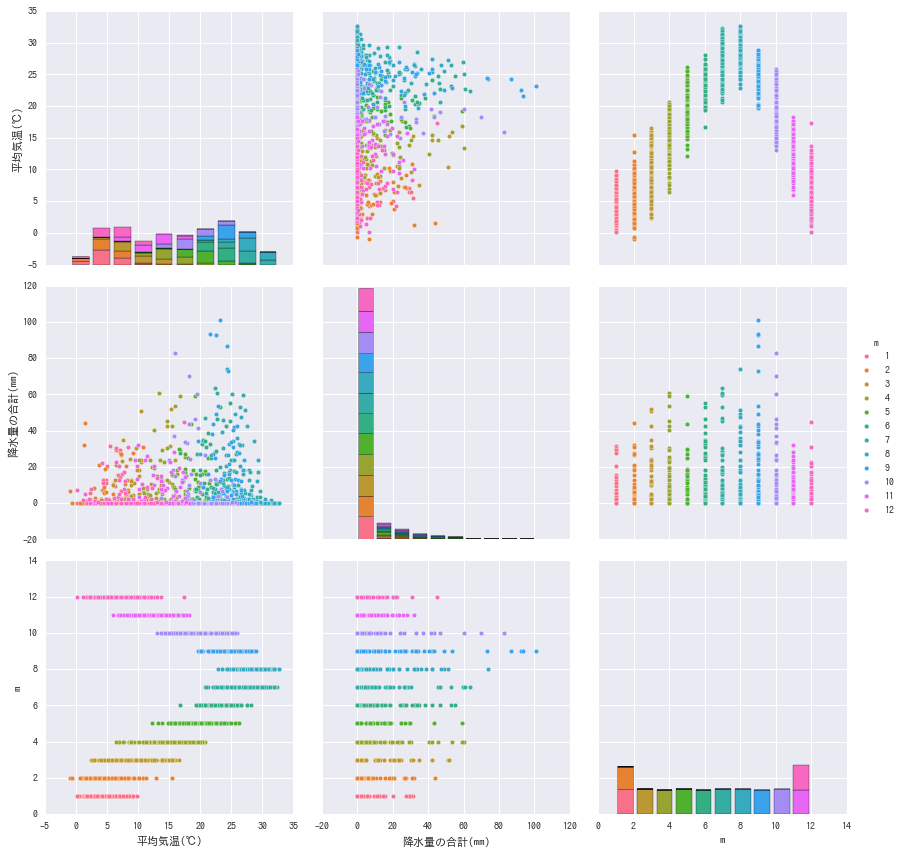
アヒル本では対角線の上と下で別のプロットを書いていたけど、正直手でやるのはちょっと面倒。変数の型とか見て自動でやるやつをそのうち作りたい。

fig, ax = plt.subplots(figsize=(20,20))
sns.violinplot(data=aichi, x="m", y =u"平均気温(℃)")
fig, ax = plt.subplots(figsize=(20,20))
sns.violinplot(data=aichi, x="m", y =u"平均気温(℃)", hue="is_rain", split=True)
plt.show()

f:id:ksknw:20161211134455p:plain

f:id:ksknw:20161211134516p:plain

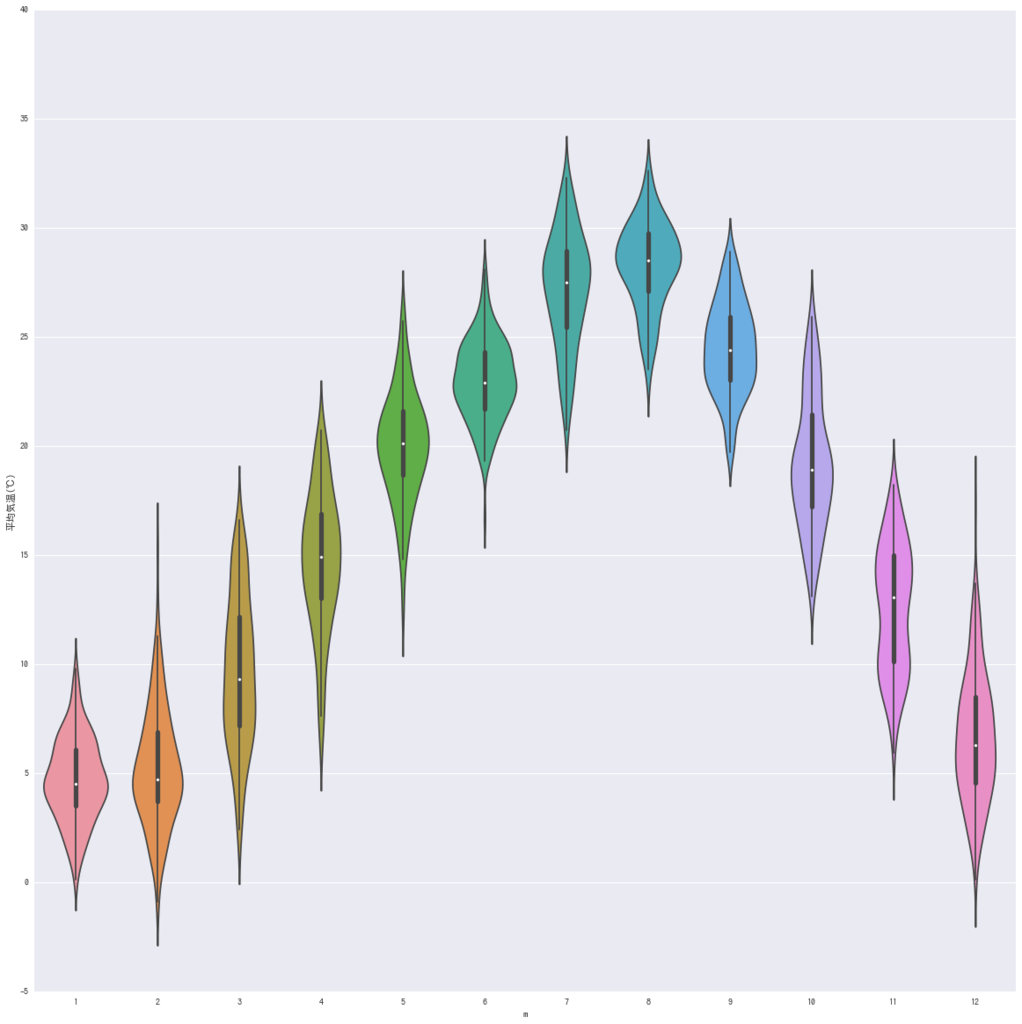
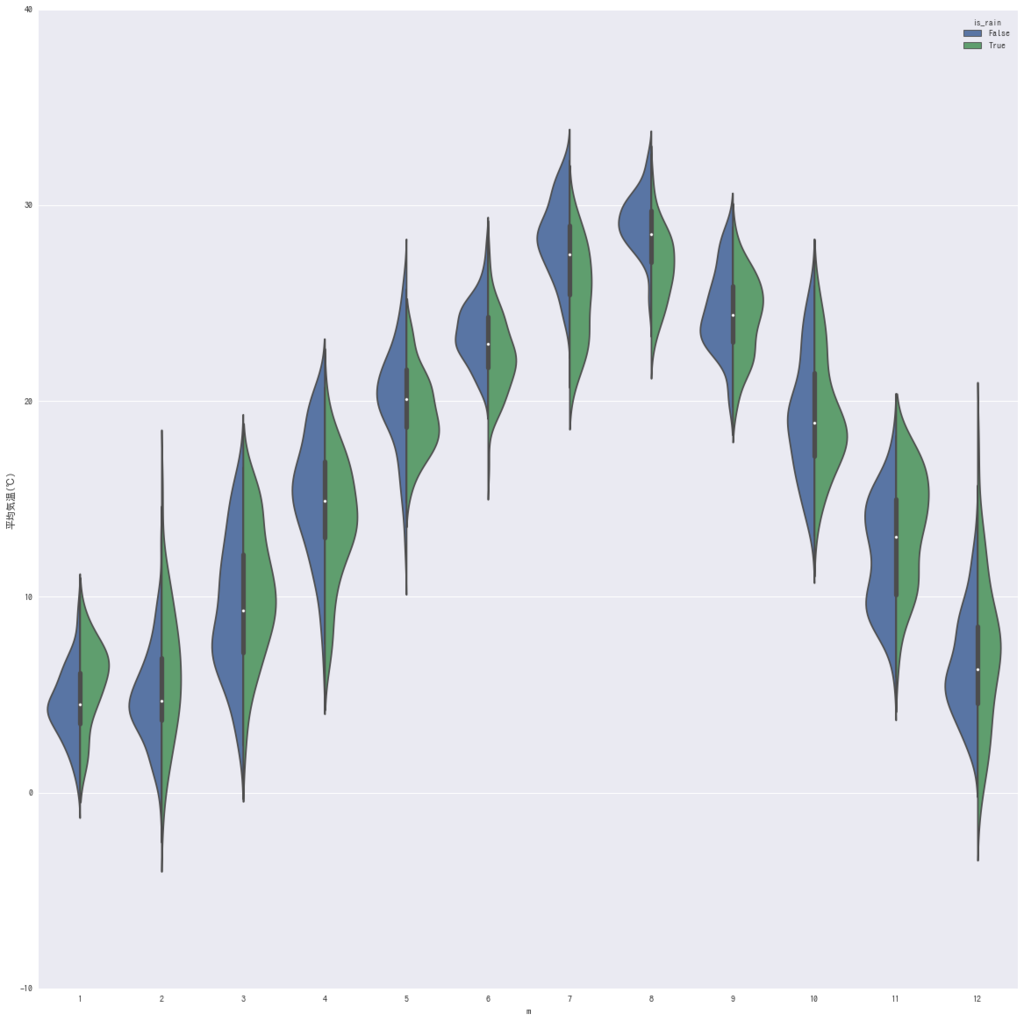
雨が降ると夏は気温が下がるけど、冬は逆に気温が高い。そりゃそうだな。

temperatures = aichi[u"平均気温(℃)"].get_values()
data = {"Y":temperatures,
       "N":len(aichi),
       "is_rain":aichi["is_rain"].astype(int).get_values()+1}

状態空間モデルでのフィッティング

アヒル本12章を見ながら、いくつかのモデルを使って気温の変動をモデル化する。

状態空間モデル(1階差分)

観測された気温( ${ \displaystyle Y }$ )は真の気温( ${ \displaystyle \mu }$ )を平均とする正規分布に従い、真の気温は、前日の真の気温を平均とする正規分布に従うというモデルを仮定する。式的には以下。

${ \displaystyle \mu_n \sim \mathcal{N}(\mu_{n-1}, s_{\mu}) }$

${ \displaystyle Y_n \sim \mathcal{N}(\mu_{n}, s_{Y}) }$

以下のようにStanでモデルを書ける。

data{
  int N;
  vector[N] Y;
}

parameters{
  vector[N] mu;
  real<lower=0> s_mu;
  real<lower=0> s_Y;
}

model{
  mu[2:N] ~ normal(mu[1:(N-1)], s_mu);
  Y ~ normal(mu, s_Y);
}

python からStanをよんでサンプリングして、色々とプロットする。

import pystan
import numpy as np
def fit(model_filename):
    fit = pystan.stan(model_filename, data=data)
    ms = fit.extract()
    fit.plot()
    return fit, ms

def fit_plot(fit, ms, list_max_x=[-1,500,100,50], ylim=None):
    mu_mean = ms["mu"].mean(axis=0)
    mu_std  = ms["mu"].std(axis=0)

    def plot_line(max_x):
        fig = plt.figure(figsize=(10,10))
        plt.plot(mu_mean[:max_x], linewidth=0.5)
        
        plt.scatter(range(len(temperatures[:max_x])), temperatures[:max_x], marker=".",# linestyle="None", 
                    c=aichi["is_rain"].get_values()[:max_x].astype(float))
    
        plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std)[:max_x], (mu_mean+mu_std)[:max_x], alpha=0.3)
        plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std*2)[:max_x], (mu_mean+mu_std*2)[:max_x], alpha=0.2)

        plt.xlim(0, len(temperatures[:max_x]))
        if not ylim==None:
            plt.ylim(*ylim)
        plt.show()
   
    for max_x in list_max_x:
        plot_line(max_x)

fit1 = fit("./model.stan") 
fit_plot(*fit1, list_max_x=[-1,100])

f:id:ksknw:20161211140401p:plain

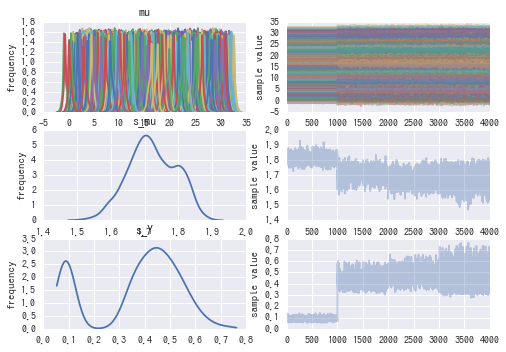
1000のあたりとか、見るからにサンプリングが安定していない感じがある。サンプリング結果を見てみる。

fit1[0]

           mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
mu[0]     12.18  6.1e-3   0.39  11.34  11.99  12.19  12.36  12.98 4000.0    1.0
mu[1]     11.84  6.0e-3   0.38  10.98  11.66  11.87  12.04  12.63 4000.0    1.0
mu[2]     10.36  6.1e-3   0.38   9.49  10.16  10.39  10.54  11.15 4000.0    1.0
mu[3]      8.21  6.5e-3   0.41   7.47   7.96   8.12   8.46   9.13 4000.0   1.05
mu[4]      9.99  6.2e-3   0.39    9.1   9.77  10.04   10.2  10.74 4000.0   1.02

mu[1825]  11.77  6.5e-3   0.41  10.85  11.53  11.87  12.04  12.48 4000.0   1.07
mu[1826]  10.97  6.1e-3   0.39  10.14  10.78  10.99  11.18  11.76 4000.0    1.0
mu[1827]   9.86  6.3e-3    0.4   9.08   9.67   9.83  10.06  10.75 4000.0    1.0
s_mu       1.72    0.04   0.07   1.59   1.67   1.72   1.78   1.85    3.0   1.71
s_Y        0.37    0.12   0.18   0.07    0.2   0.42   0.49   0.63    2.0   3.15
lp__     -622.4  903.47 1277.7  -1830  -1483  -1218 121.56 1970.3    2.0   5.28

アヒル本によると、

n_effはStanが自己相関等から判断した実効的なMCMCサンプル数である。

とあるので、今回のサンプリングではs_muやs_Yはまともにサンプリングされていないことがわかる。

また、Rhatはパラメータが収束したかどうかを表す値であり、

「chain数が3以上ですべてのパラメータでRhat < 1.1 となること」を「収束した」と見なすことにする。

とある。ということで、このモデルではうまく収束しなかった。サンプリング数を増やしたりしてもいいのかもしれないが、今回は別のモデルを作ることにする。

状態空間モデル(2階差分)

真の気温の変化はその前の日の真の気温の変化を平均とする正規分布に従うというモデル。式的には以下。

${ \displaystyle \mu_n-\mu_{n-1} \sim \mathcal{N}(\mu_{n-1}-\mu_{n-2}, s_{\mu}) }$

${ \displaystyle Y_n \sim \mathcal{N}(\mu_{n}, s_{Y}) }$

Stanのコードは以下。

data{
  int N;
  vector[N] Y;
}

parameters{
  vector[N] mu;
  real<lower=0> s_mu;
  real<lower=0> s_Y;
}

model{
  mu[3:N] ~ normal(2 * mu[2:(N-1)] - mu[1:(N-2)], s_mu);
  Y ~ normal(mu, s_Y);
}

サンプリングする。

fit2 = fit("./model2.stan") 
fit_plot(*fit2, list_max_x=[-1,100])

f:id:ksknw:20161211140436p:plain

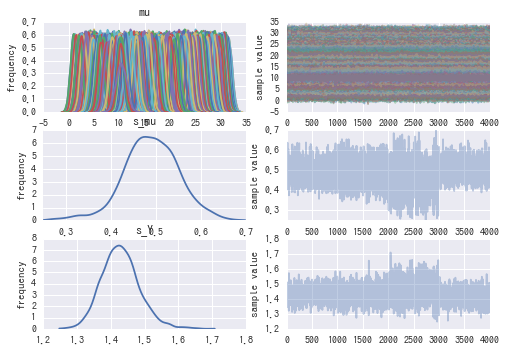
サンプリング結果

fit2[0]

           mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
mu[0]     12.12    0.02   1.06  10.07  11.42  12.13  12.83  14.17 4000.0    1.0
mu[1]     11.26    0.01   0.76   9.76  10.75  11.25  11.78  12.75 4000.0    1.0
mu[2]     10.41    0.01   0.67   9.12   9.95  10.41  10.86  11.73 4000.0    1.0
mu[3]      9.64    0.01   0.68   8.28   9.19   9.65  10.09  10.97 4000.0    1.0
mu[4]      9.04    0.01   0.68    7.7   8.59   9.04   9.49  10.38 4000.0    1.0

mu[1825]  10.28    0.01   0.67   8.99   9.82  10.28  10.73  11.59 4000.0    1.0
mu[1826]   10.4    0.01   0.75   8.94    9.9  10.38   10.9  11.89 4000.0    1.0
mu[1827]  10.42    0.02   1.04   8.42   9.72  10.42  11.14  12.39 4000.0    1.0
s_mu       0.49  9.5e-3   0.06   0.35   0.45   0.49   0.53   0.61   42.0    1.1
s_Y        1.43  7.5e-3   0.06   1.33   1.39   1.43   1.46   1.55   55.0   1.07
lp__      -1158   28.55 180.58  -1459  -1281  -1171  -1060 -711.0   40.0   1.09

Rhatの値を見てみる1.1ギリギリという感じ。 n_effも50とかしかないので、厳しそう。

一応 $\mu$ のベイズ信頼区間のグラフを見る。白丸が晴れの日、黒丸は雨の日を表す。濃い青は68%ぐらい、薄い青は95%ぐらい。青線は平均値を表す。

f:id:ksknw:20161211181516p:plain

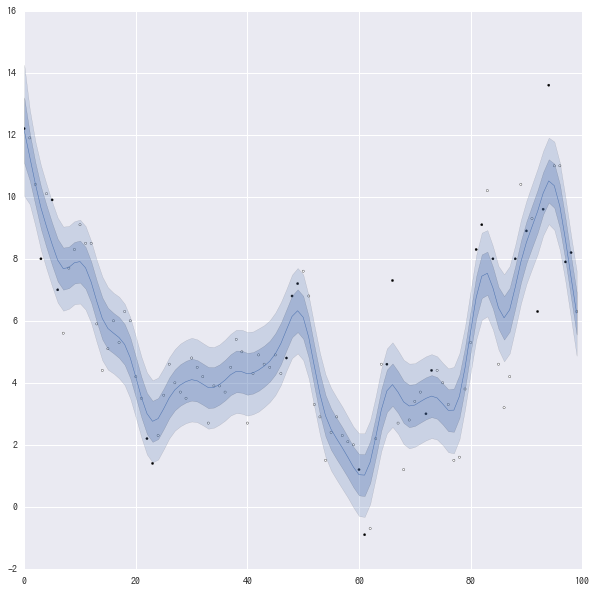
なんとなく雨の日が上手くあっていないような気がする。雨が降ると前日との温度差が大きくなることが予想されるので、そのへんのモデルをちゃんと作ったほうが良さそう。

状態空間モデル(2階差分降水量を考慮するモデル)

はじめの方に描いたグラフなどから天気を考慮する必要がありそう。そこで、この題材に対するモチベーションとモデルの当てはまりから以下のようなモデルを仮定する。

${ \displaystyle \mu_n-\mu_{n-1} \sim \mathcal{N}(\mu_{n-1}-\mu_{n-2}, s_{\mu}) }$

雨のとき

${ \displaystyle Y_n \sim \mathcal{N}(\mu_{n}, s_{Y|\mathrm{rain}}) }$

雨がふらなかったとき

${ \displaystyle Y_n \sim \mathcal{N}(\mu_{n}, s_{Y|\mathrm{no\ rain}}) }$

雨が振った日と振らなかった日では、真の気温から観測値へ乱数の分散が変わるというモデル本当は分散だけでなく平均も変わったほうがいい気がするが、その変わり方が季節ごとに違うので面倒でやめた。

fit3 = fit("./model3.stan") 
fit_plot(*fit3, list_max_x=[-1,100])

f:id:ksknw:20161211181548p:plain

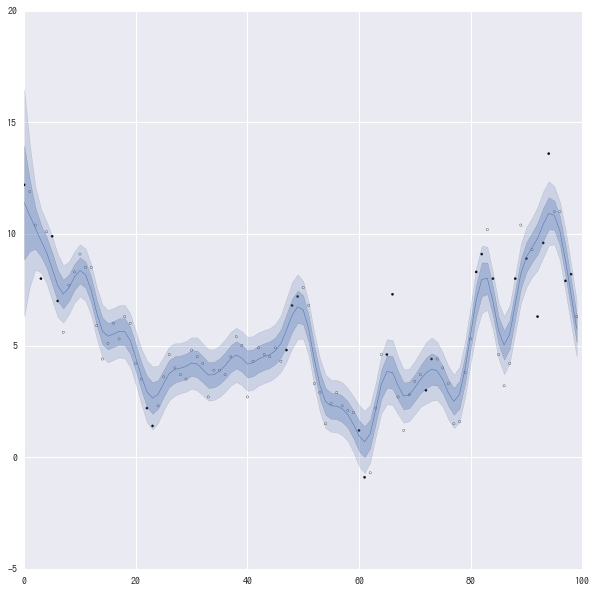
fit3[0]

       mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
mu[0]     11.41    0.04   2.55   6.51   9.72  11.38  13.13   16.4 4000.0    1.0
mu[1]     10.83    0.03   1.59   7.72   9.74  10.84   11.9  13.97 4000.0    1.0
mu[2]     10.26    0.01   0.93   8.46   9.64  10.25  10.89  12.09 4000.0    1.0
mu[3]      9.71    0.01   0.72   8.32   9.22    9.7  10.18  11.11 4000.0    1.0

mu[1826]  10.52  9.9e-3   0.63   9.31  10.08  10.52  10.96  11.77 4000.0    1.0
mu[1827]  10.38    0.01   0.88   8.65   9.78  10.39  10.99  12.07 4000.0    1.0
s_mu       0.69  7.5e-3   0.07   0.55   0.64   0.69   0.74   0.82   88.0   1.03
s_Y[0]     1.06  5.5e-3   0.06   0.95   1.01   1.05    1.1   1.18  123.0   1.02
s_Y[1]      1.7  2.9e-3   0.07   1.57   1.65    1.7   1.75   1.84  583.0   1.01
lp__      -1508    13.2 122.38  -1712  -1595  -1520  -1433  -1247   86.0   1.03

前のモデルよりちゃんと収束してる感はある。 s_Y[1]が雨が降った日なので、雨の日は晴れの日よりも、真の気温からの分散が大きくなる。

前のモデルとの違いがぱっとわからないので、重ねてグラフをかく。

fig = plt.figure(figsize=(10,10))
max_x = 100
colors = ["b", "g"]
for i,ms in enumerate([fit2[1], fit3[1]]): 
    mu_mean = ms["mu"].mean(axis=0)
    mu_std  = ms["mu"].std(axis=0)

    plt.plot(mu_mean[:max_x], linewidth=0.5)    
    plt.scatter(range(len(temperatures[:max_x])), temperatures[:max_x], marker=".",# linestyle="None", 
                c=aichi["is_rain"].get_values()[:max_x].astype(float))
    
    #plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std)[:max_x], (mu_mean+mu_std)[:max_x], alpha=0.3)
    plt.fill_between(range(len(mu_mean[:max_x])), (mu_mean-mu_std*2)[:max_x], (mu_mean+mu_std*2)[:max_x], alpha=0.2
                    ,color=colors[i])

plt.xlim(0, len(temperatures[:max_x]))
plt.ylim([-5, 20])
plt.show()

f:id:ksknw:20161211141729p:plain

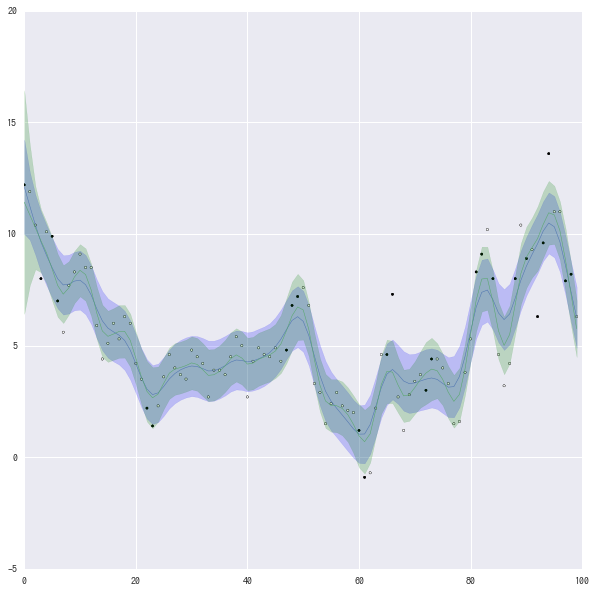
青が単純な2階差分、緑が雨で条件わけしたモデル。正直良くなっているのかどうかよくわからない。

まとめと今後

アヒル本を参考にして、気温変動のモデリングを行った。 Stanの使い方はなんとなくわかってきたけど、統計的に正しいのかとか、いまいちよくわかっていない。

今回は年ごとの関係を考慮しないでモデルを作った。 sinとかでモデル化できそうな気がする。また、雨の日と晴れの日でsinの強さが変わるようにすると、もっといい感じにモデル化できるように思う。

Stanでまだわかってないことの1つにディリクレ混合過程がある。アヒル本には載っていなかったけど、このへんを見ながらやってみたい。

fit.plot()のfig_sizeを大きくしたいんだけど、どうやらpython側でなくstan側からプロットされている(?)ようで、いまいちやり方がわからなかった。

(この記事には、グラフを死ぬほどかかないといけないという認識があまり反映されていないのではないか。)

参考

2016-08-04

jupyter notebookで触れるプロットを描く

回転できる3Dプロット
スライドバーつき
もっと綺麗なグラフを描く
参考

昔、Emacsから使えないからjupyter notebookは使わないという旨の記事を書いた。実際まだ、Emacsからは使えていないけど、最近はだいたいのコードをEmacs+pythonで書いて、実行やグラフを描く部分をjupyter notebookでやるということをよくやっている。

jupyter notebook内にグラフを描く方法として

%matplotlib inline

という文を実行しておくという方法がある。

大体の場合にはこれで間に合うが、3Dグラフを回したり、アニメーションを動かしたりすることができなかった。調べてみると他にも色々できることがわかったのでまとめる。この記事では以下のようなプロットを描く。

回転できる3D
アニメーション
スライドバー付き
もっと綺麗なグラフを描く

markdownで出力すると全く触れなくなったので動画を作った。

www.youtube.com

回転できる3Dプロット

%matplotlib inline

でプロットを作成すると、ノートブックの中に画像として出力されてしまうので回せない。

%matplotlib notebook

を使うとノートブックの外に出力したときと同じように、インタラクティブなグラフが描ける。こちらの3次元プロットを例として描く。

%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-3, 3, 0.25)
y = np.arange(-3, 3, 0.25)
X, Y = np.meshgrid(x, y)
Z = np.sin(X)+ np.cos(Y)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(X,Y,Z)

plt.show()

f:id:ksknw:20160804225927p:plain

スライドバーつき

ipywidgetsというやつを使えばできる。 jupyter notebookをインストールしただけで使おうとすると以下のコマンドを実行するように表示されたので、おとなしく従うと動くようになった。

sudo jupyter nbextension enable --py --sys-prefix widgetsnbextension

以下を実行すると、スライドバーが表示される。このバーをいじると変数の値が動的に変わるので、コールバックにプロットを登録しておくと、スライドバーをいじるだけで勝手にプロットが変わる。

自分の環境では

%matplotlib notebook

とするとカクカクでいまいちだったが、

%matplotlib inline

にするといい感じ。

%matplotlib inline
from ipywidgets import interact
import numpy as np

def scatter(num_data):
    x = range(num_data)
    y = [np.sin(t/5.0) for t in x]
    plt.plot(x, y)
    plt.show()

interact(scatter, num_data=(1,200, 1), value=2)

f:id:ksknw:20160804225709p:plain

ipywidgetsには他にもボタンとかプログレスバーとか色々あって、ノートを簡単なアプリにできる。

%matplotlib inline

import pylab as plt
import time
from ipywidgets import FloatProgress
from IPython import display

prg = FloatProgress(min=0, max=99, value=1)
display.display(prg)

for i in range(100):
    prg.value = i
    time.sleep(0.01)

もっと綺麗なグラフを描く

matplotlibではなくて、plotlyというライブラリを使えばできる。 matplotlibと書き方が結構違うので、改めて覚えてまでやるほどかと言われると微妙だが、グラフは綺麗でかっこいい。コードやグラフ、データをオンラインで共有したりもできるらしい。

デモのサイトを見ていると可能性を感じる。

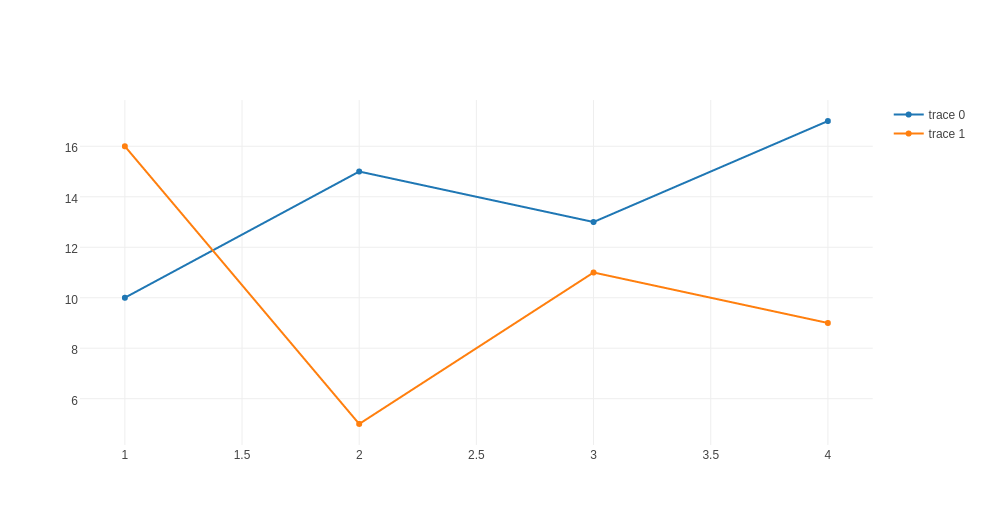
from plotly.offline import iplot, init_notebook_mode
import plotly.plotly as py
from plotly.graph_objs import Scatter, Data


init_notebook_mode(connected=True) 

trace0 = Scatter(
    x=[1, 2, 3, 4],
    y=[10, 15, 13, 17]
)

trace1 = Scatter(
    x=[1, 2, 3, 4],
    y=[16, 5, 11, 9]
)

data = Data([trace0, trace1])
unique_url = iplot(data, filename = 'basic-line')

f:id:ksknw:20160804230515p:plain

概要

はじめに

Dynamic Time Warping

長さが異なる時系列の距離(的なもの)

位相をだんだんずらしていったときの挙動

実データ（国内１週間の気温データ）

おまけ

tSNE

おわりに

参考

はじめに

環境

ベクトルと行列ベクトル

トレース，行列式と逆行列

ベクトルの内積

行列とベクトルの積

行列の積

要素ごとの積 (アダマール積)

ベクトルから行列 (テンソル積 ?)

その他，関係ありそうだけど使ってない関数

おわりに

概要

はじめに

MovieLensデータ

1次交互勾配降下法

擬似2次交互勾配法

制約付きの最適化

欠損値をちゃんとやる

除外する方法

補完する方法

ベクトルをみる

まとめ

参考

はじめに

環境

その他

今後の課題

参考

概要

はじめに

ツイッターデータのダウンロード

非正規化グラフラプラシアンに基づくスペクトルクラスタリング

対称正規化グラフラプラシアンに基づくスペクトルクラスタリング

酔歩正規化グラフラプラシアン

確率的ブロックモデルによる非対称データクラスタリング

追記(2017年1月5日)

追記(2017年4月)

おわりに

参考

はじめに

データ

状態空間モデルでのフィッティング

状態空間モデル(1階差分)

状態空間モデル(2階差分)

状態空間モデル(2階差分 降水量を考慮するモデル)

まとめと今後

参考

回転できる3Dプロット

スライドバーつき

もっと綺麗なグラフを描く

参考

ベクトルと行列ベクトル ${\bf x},A$

トレース，行列式と逆行列 $\mathrm{trace(A)}, \mathrm{det}(A), A^{-1}$

ベクトルの内積 $x・x$

行列とベクトルの積 $Ax$

行列の積 $AA, A^\top A$

要素ごとの積 (アダマール積) $C_{ij} = A_{ij}B_{ij}$

ベクトルから行列 (テンソル積 ?) $B_{ij} = x_ix_j, B_{ijk} = A_{ij}x_{k}$

追記(2017年4月)　

状態空間モデル(2階差分降水量を考慮するモデル)